【NOTE】注意

本ノートは MLP（多層パーセプトロン）の内容を前提として記述する。

RNN とは

RNN = Recurrent Neural Network

自然言語処理や音声信号など、時系列データ処理の分野で高い性能を発揮するニューラルネットワークの1種。

概観

下図に RNN の概観を示す。
ここでは、各時刻のデータ $\boldsymbol{x}_1,\cdots,\boldsymbol{x}_t$ ごとに対応する出力値 $\boldsymbol{y}_1,\cdots,\boldsymbol{y}_t$ を得る系列ラベリングの問題を想定する。
（例：文章データの単語ごとの品詞分類）

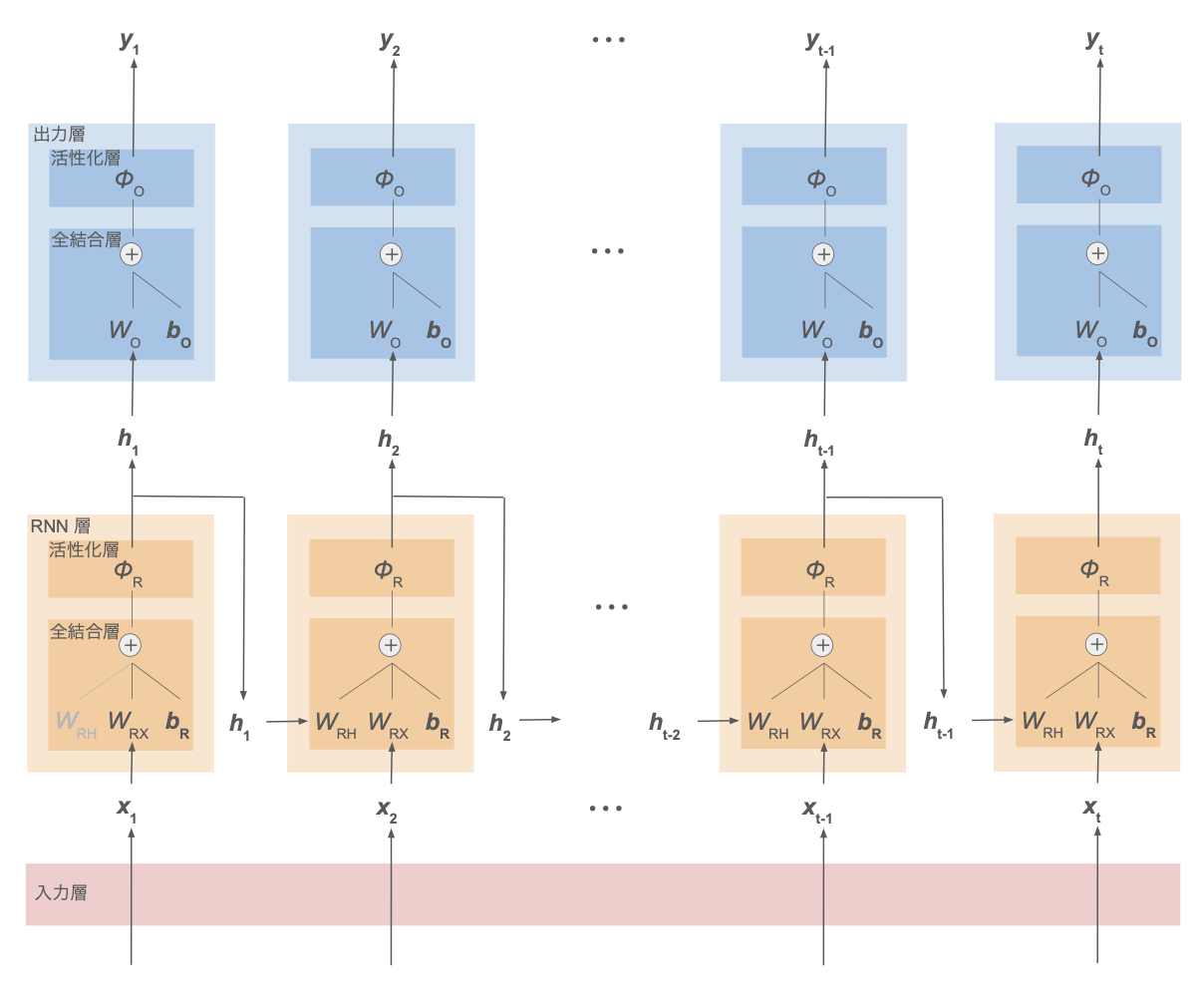
rnn_overview_many2many

処理層 説明
入力層 MLP（多層パーセプトロン）を参照
出力層 MLP（多層パーセプトロン）を参照
全結合層 MLP（多層パーセプトロン）を参照
活性化層 MLP（多層パーセプトロン）を参照
RNN 層 ・時刻 $t$ の入力データ $\boldsymbol{x}t$ と重み行列 $W{RX}$ の積
・1つ前の時刻 $t-1$ の RNN 層の出力（= 隠れ状態）$\boldsymbol{h}{t-1}$ と重み行列 $W{RH}$ の積
・バイアス $\boldsymbol{b}_R$
の和を取った後に活性化関数を適用し、時刻 $t$ の隠れ状態 $\boldsymbol{h}_t$ を計算

※ RNN 層・出力層それぞれについて、重み $W_{RH},W_{RX},W_O$、バイアス $\boldsymbol{b}_R,\boldsymbol{b}_O$ は時刻によらず共通のパラメータ

時刻 $t$ の RNN 層にて、その時刻のデータだけでなく前時刻 $t-1$ の隠れ状態 $\boldsymbol{h}{t-1}$ も入力に加えることで、過去の時系列情報をモデルに含めることができる。
前時刻 $t-1$ の RNN 層でも同様に時刻 $t-2$ の隠れ状態 $\boldsymbol{h}{t-2}$ を入力としているので、$\boldsymbol{h}_{t-1}$ には時刻 $t-2$ の情報も含まれる。
→ したがって再帰的に、$\boldsymbol{h}_t$ はそれ以前の時刻 $1, 2, \cdots, t-1, t$ の情報を含むことになる。

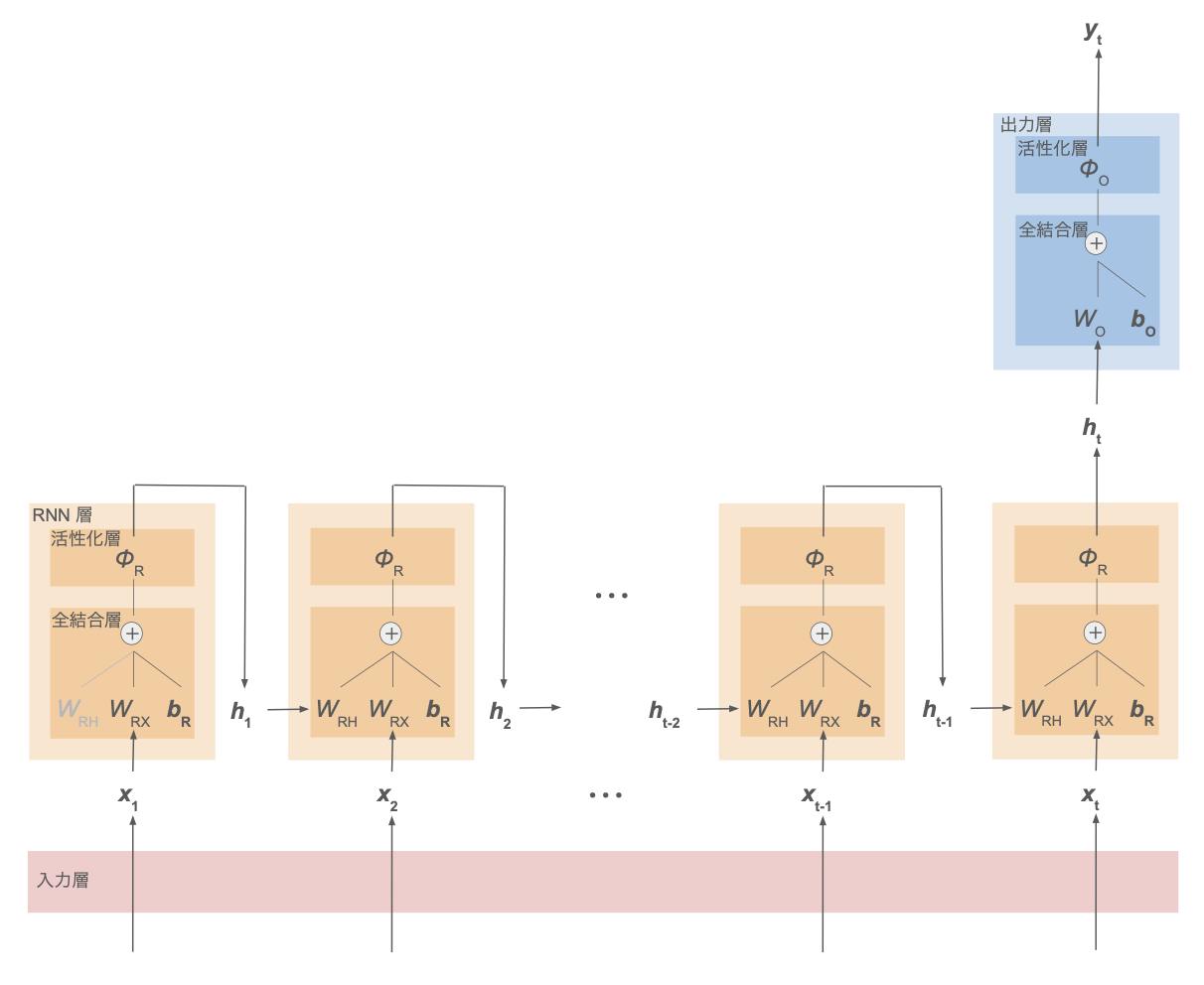
同様に、時系列 $\boldsymbol{x}_1,\cdots,\boldsymbol{x}_t$ に対して1つの出力 $\boldsymbol{y}$ を得る問題の場合の RNN を下図に示す。
（例：文章全体のクラス分類）

rnn_overview_many2one

これらも含めて、RNN のネットワークには以下のような分類がある。

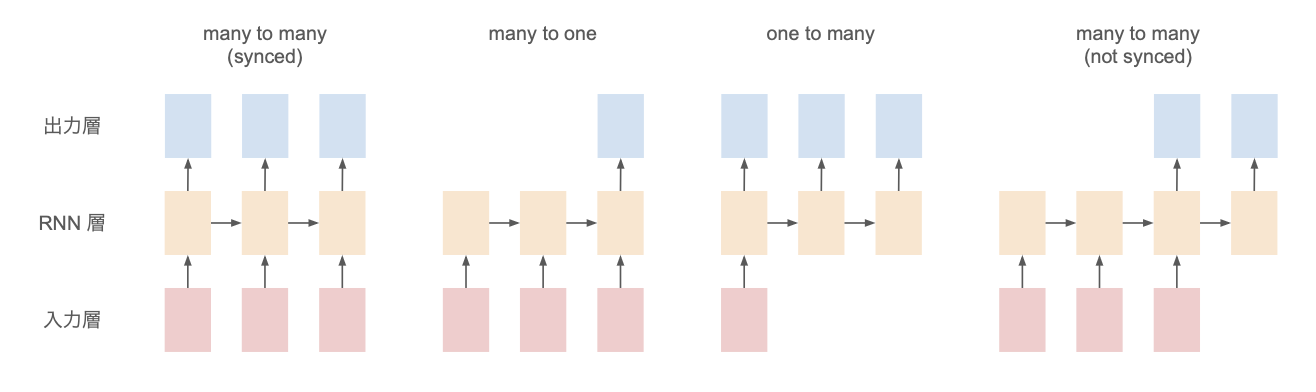
rnn_types

  • many to many
    • synced：品詞分類など
    • not synced：機械翻訳など
  • many to one：文章分類など
  • one to many：画像のキャプション生成

また、RNN 層と出力層の間に多層パーセプトロンの隠れ層を挟んでディープなネットワークにすることもできる：

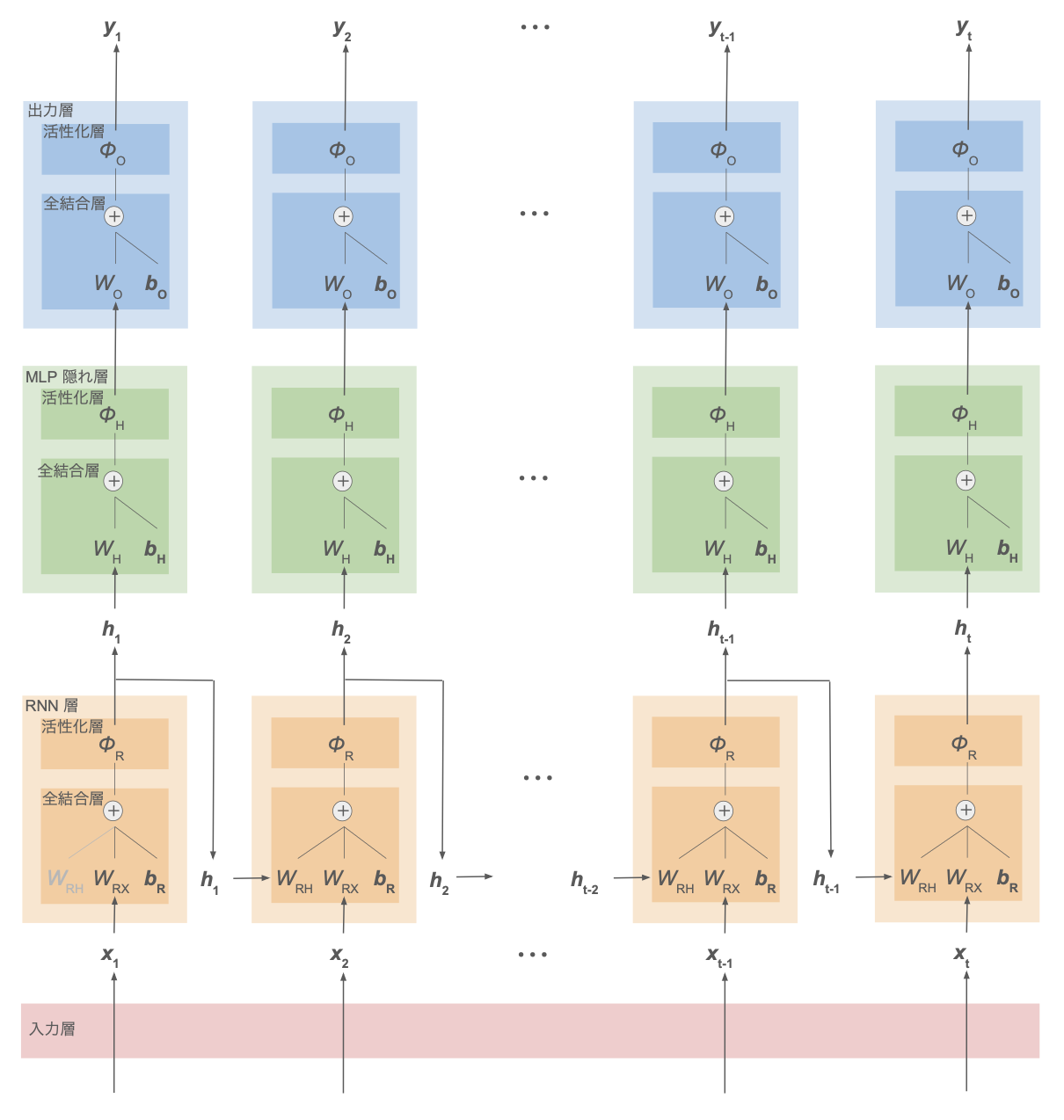
rnn_overview_hidden

RNN 層の処理

順方向の処理

RNN 層では、その時刻 $t$ の時系列データ $\boldsymbol{x}t$ と、1ステップ前の時刻の隠れ状態 $\boldsymbol{h}{t-1}$ それぞれに重みをかけてバイアス $\boldsymbol{b}$ を加えて活性化関数 $\phi_R$ を適用し、過去の時系列情報を含む隠れ状態 $\boldsymbol{h}_t$ を生成する：

\[\boldsymbol{h}_t := \phi_R( W_{RX} \boldsymbol{x}_t + W_{RH} \boldsymbol{h}_{t-1} + \boldsymbol{b} ) \tag{1}\]

ここで、ベクトル $\boldsymbol{h}t,\boldsymbol{h}{t-1}, \boldsymbol{x}_t, \boldsymbol{b}$ はすべて列ベクトルとして扱っている。

入力 $\boldsymbol{x}_t$ の次元を $N$、隠れ状態 $\boldsymbol{h}_t$ やバイアス $\boldsymbol{b}$ の次元を $H$ とすれば、

  • $W_{RX}$：$H\times N$ 行列
  • $W_{RH}$：$H \times H$ 行列

また、最初の時系列データ $\boldsymbol{x}_1$ を入力とするときは「1ステップ前の時刻の隠れ状態」が存在しないため、ゼロベクトルを入力としておく。

誤差逆伝播による学習

RNN 層の活性化層の誤差逆伝播に関しては、基本的に多層パーセプトロン（MLP）と同様のためそちらを参照。
ただし many to many のように、活性化層の出力が次の時間ステップの RNN 層だけでなく全結合層等にも枝分かれして渡される場合、枝分かれしたそれぞれの誤差を足し合わせて逆伝播させる。

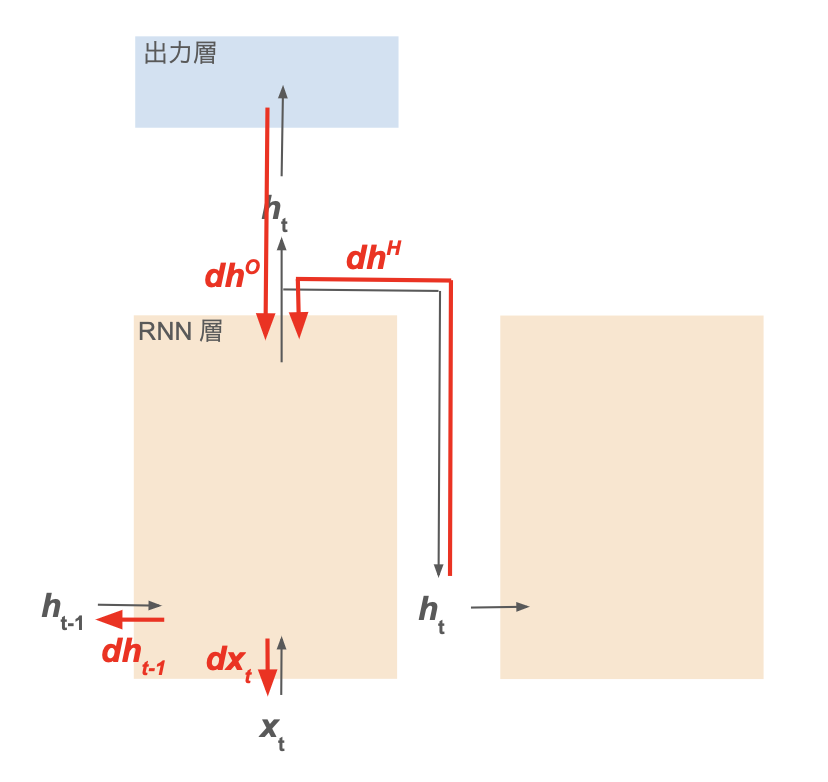
rnn_bp

ここでは、RNN 層の全結合層について記述する。

入力変数

変数 説明
$\boldsymbol{x}_t$ 時刻 $t$ の時系列データ。$N$ 次元ベクトル
$\boldsymbol{h}_{t-1}$ 1ステップ前の時刻の RNN 層で計算した隠れ状態。$H$ 次元ベクトル
$W_{RX}$ 時系列データ $\boldsymbol{x}_t$ にかける重み。$H\times N$ 行列
$W_{RH}$ 1ステップ前の隠れ状態 $\boldsymbol{h}_{t-1}$ にかける重み。$H\times H$ 行列
$\boldsymbol{b}$ バイアス項。$H$ 次元ベクトル

出力変数

\[\begin{eqnarray} \boldsymbol{z} &:=& W_{RX} \boldsymbol{x}_t + W_{RH} \boldsymbol{h}_{t-1} + \boldsymbol{b} \\ z_i &=& \sum_j W_{RX,ij} x_{t,j} + \sum_j W_{RH,ij} h_{t-1,j} + b_i \end{eqnarray} \tag{2}\]

コスト関数の勾配

$(2)$ 式より、

\[\begin{eqnarray} \cfrac{\partial z_i}{\partial x_{t,j}} &=& W_{RX,ij} \\ \cfrac{\partial z_i}{\partial h_{t-1,j}} &=& W_{RH,ij} \\ \cfrac{\partial z_i}{\partial W_{RX,kl}} &=& \delta_{ik} x_{t,l} \\ \cfrac{\partial z_i}{\partial W_{RH,kl}} &=& \delta_{ik} h_{t-1,l} \\ \cfrac{\partial z_i}{\partial b_j} &=& \delta_{ij} \end{eqnarray}\]

ここで、$\delta_{ik}$ はクロネッカーのデルタ（$i=k$ のときのみ1、それ以外は0）。

ゆえに、RNN 層のパラメータに関するコスト関数 $J$ の勾配は

\[\begin{eqnarray} \cfrac{\partial J}{\partial x_{t,i}} &=& \sum_j \cfrac{\partial J}{\partial z_j}\cfrac{\partial z_j}{\partial x_{t,i}} = \sum_j \cfrac{\partial J}{\partial z_j} W_{RX,ji} = \sum_j W_{RX,ij}^T \cfrac{\partial J}{\partial z_j} = \left( W_{RX}^T \cfrac{\partial J}{\partial \boldsymbol{z}} \right)_i \\ \cfrac{\partial J}{\partial h_{t-1,i}} &=& \sum_j \cfrac{\partial J}{\partial z_j}\cfrac{\partial z_j}{\partial h_{t-1,i}} = \sum_j \cfrac{\partial J}{\partial z_j} W_{RH,ji} = \sum_j W_{RH,ij}^T \cfrac{\partial J}{\partial z_j} = \left( W_{RH}^T \cfrac{\partial J}{\partial \boldsymbol{z}} \right)_i \\ \cfrac{\partial J}{\partial W_{RX,kl}} &=& \sum_j \cfrac{\partial J}{\partial z_j}\cfrac{\partial z_j}{\partial W_{RX,kl}} = \sum_j \cfrac{\partial J}{\partial z_j} \delta_{jk} x_{t,l} = \cfrac{\partial J}{\partial z_k} x_{t,l} = \left( \cfrac{\partial J}{\partial \boldsymbol{z}} \boldsymbol{x}_t^T \right)_{kl} \\ \cfrac{\partial J}{\partial W_{HX,kl}} &=& \sum_j \cfrac{\partial J}{\partial z_j}\cfrac{\partial z_j}{\partial W_{HX,kl}} = \sum_j \cfrac{\partial J}{\partial z_j} \delta_{jk} h_{t-1,l} = \cfrac{\partial J}{\partial z_k} h_{t-1,l} = \left( \cfrac{\partial J}{\partial \boldsymbol{z}} \boldsymbol{h}_{t-1}^T \right)_{kl} \\ \cfrac{\partial J}{\partial b_i} &=& \sum_j \cfrac{\partial J}{\partial z_j} \cfrac{\partial z_j}{\partial b_i} = \sum_j \cfrac{\partial J}{\partial z_i} \delta_{ji} = \cfrac{\partial J}{\partial z_i} = \left( \cfrac{\partial J}{\partial \boldsymbol{z}} \right)_i \end{eqnarray}\]

改善のための手法

Layer Normalization

多層パーセプトロン（MLP）では、同じ特徴量ごとにミニバッチ間で 平均・標準偏差を計算してデータを標準化する Batch Normalization について記述した。

RNN や Transformer では、勾配爆発・勾配消失の緩和手法として、Layer Normalization がよく利用される。
この手法では、特徴量間で 平均・標準偏差を計算してデータを標準化する。 すなわち、バッチ内の他のサンプルに依存せず、個別のサンプル内で標準化を行う。

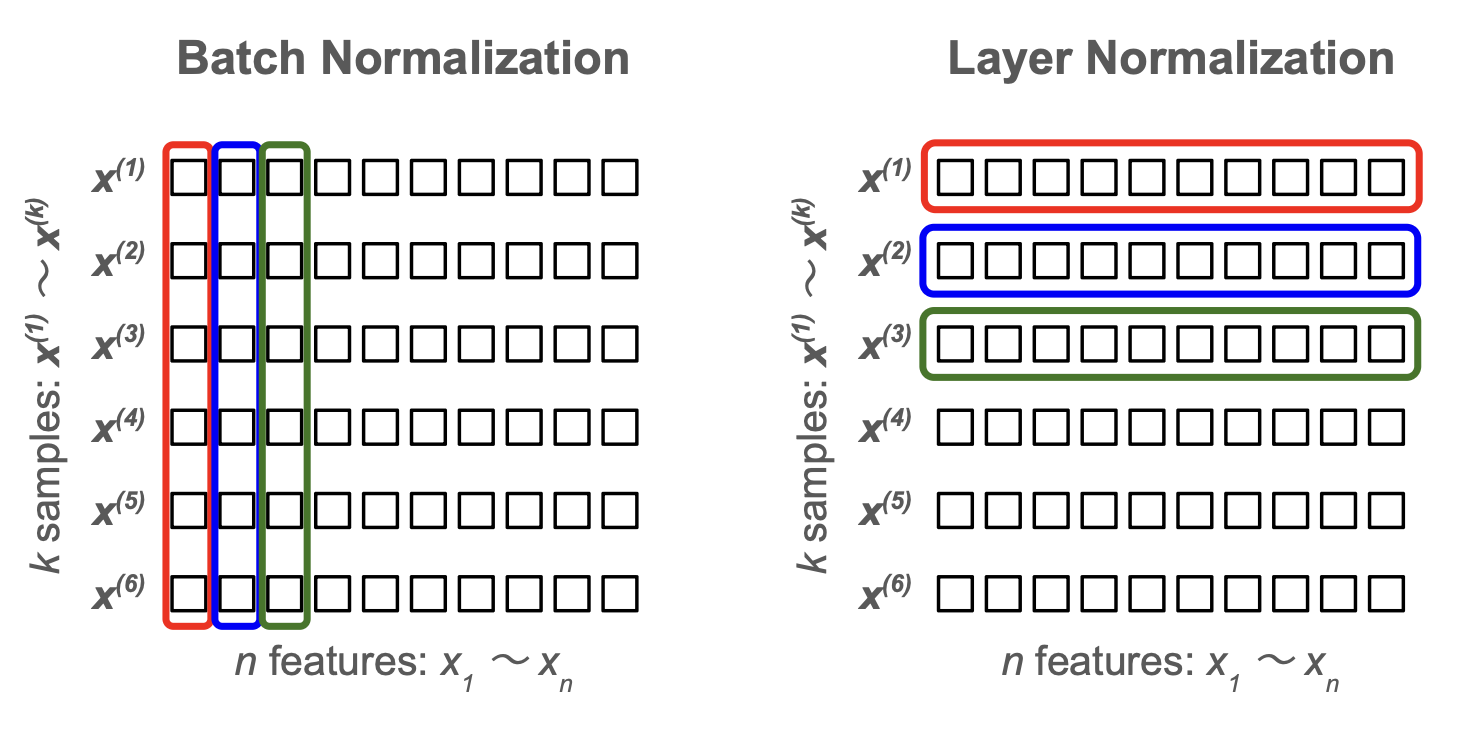
rnn_layer-normalization

Batch Normalization (BN) も Layer Normalization (LN) も値の範囲を一定に抑えて学習を安定させるための手法だが、時系列データは系列ごとに長さが異なることも多く、BN でバッチ間の統計を安定して取ることが難しい。 そのため、時系列データを扱う RNN においては Layer Normalization が適する。

入力変数

変数 説明
$\boldsymbol{x}$ 前層の出力。ミニバッチ学習の場合は、そのうちの1つのデータサンプル
$N_f$ $\boldsymbol{x}$ の次元（特徴量次元）
$\boldsymbol{\gamma}$ $\boldsymbol{x}$ と同じ $N_f$ 次元の調整用変数（重み）
$\boldsymbol{\beta}$ $\boldsymbol{x}$ と同じ $N_f$ 次元の調整用変数（バイアス）

中間変数

変数 説明
$\mu$ $\boldsymbol{x}$ の特徴量の値の平均
$\sigma$ $\boldsymbol{x}$ の特徴量の値の標準偏差
$\hat{\boldsymbol{x}}$ $\boldsymbol{x}$ を $\mu, \sigma$ で標準化したもの
\[\begin{eqnarray} \mu &:=& \cfrac{1}{N_f} \displaystyle \sum_k x_k \\ \sigma^2 &:=& \cfrac{1}{N_f} \displaystyle \sum_k \left( x_k - \mu \right)^2 \\ \hat{\boldsymbol{x}} &:=& \cfrac{\boldsymbol{x} - \mu}{\sqrt{\sigma^2 + \varepsilon}} \end{eqnarray}\]

※ ベクトルの2乗は各成分を2乗している（アダマール積）
※ $\varepsilon$ は $10^{-14}$ などゼロ除算を防ぐための非常に小さい正の数

出力変数

\[\begin{eqnarray} \boldsymbol{z} &:=& \boldsymbol{\gamma} \odot \hat{\boldsymbol{x}} + \boldsymbol{\beta} \\ z_i &:=& \gamma_i x_i + \beta_i \end{eqnarray}\]

ここで、$\odot$ は同じ成分同士の積を取るアダマール積を表す。

勾配の導出

\[\begin{eqnarray} \cfrac{\partial \mu}{\partial x_i} &=& \cfrac{1}{N_f} \\ \cfrac{\partial \sigma^2}{\partial x_i} &=& \cfrac{2}{N_f} \left( x_i - \mu \right) \end{eqnarray}\]

と定義式から計算できるから、

\[\begin{eqnarray} \cfrac{\partial \hat{x}_k}{\partial x_i} &=& \cfrac{1}{\sqrt{\sigma^2 + \varepsilon}} \delta_{ki} - \cfrac{\partial \mu}{\partial x_i} \cfrac{1}{\sqrt{\sigma^2 + \varepsilon}} - \cfrac{\partial \sigma^2}{\partial x_i} \cfrac{x_k - \mu}{2 \left( \sqrt{\sigma^2 + \varepsilon} \right)^3} \\ &=& \cfrac{1}{\sqrt{\sigma^2 + \varepsilon}} \delta_{ki} - \cfrac{1}{N_f} \cfrac{1}{\sqrt{\sigma^2 + \varepsilon}} - \cfrac{2}{N_f} (x_i - \mu) \cfrac{x_k - \mu}{2\left( \sqrt{\sigma^2 + \varepsilon} \right)^3} \\ &=& \cfrac{1}{\sqrt{\sigma^2 + \varepsilon}} \left\{ \delta_{ki} - \cfrac{1}{N_f} - \cfrac{1}{N_f} \cfrac{x_i - \mu}{\sqrt{\sigma^2 + \varepsilon}} \cfrac{x_k - \mu}{\sqrt{\sigma^2 + \varepsilon}} \right\} \\ &=& \cfrac{1}{\sqrt{\sigma^2 + \varepsilon}} \left( \delta_{ki} - \cfrac{1}{N_f} - \cfrac{1}{N_f} \hat{x}_i \hat{x}_k \right) \end{eqnarray}\]

よって

\[\begin{eqnarray} \cfrac{\partial J}{\partial \gamma_i} &=& \displaystyle \sum_k \cfrac{\partial J}{\partial z_k} \cfrac{\partial z_k}{\partial \gamma_i} = \displaystyle \sum_k \cfrac{\partial J}{\partial z_k} \delta_{ki} \hat{x}_i = \cfrac{\partial J}{\partial z_i} \hat{x}_i = \left( \cfrac{\partial J}{\partial \boldsymbol{z}} \odot \boldsymbol{\hat{x}} \right)_i \\ \\ \cfrac{\partial J}{\partial \beta_i} &=& \displaystyle \sum_k \cfrac{\partial J}{\partial z_k} \cfrac{\partial z_k}{\partial \beta_i} = \displaystyle \sum_k \cfrac{\partial J}{\partial z_k} \delta_{ki} = \cfrac{\partial J}{\partial z_i} \\ \\ \cfrac{\partial J}{\partial x_i} &=& \sum_k \cfrac{\partial J}{\partial z_k} \cfrac{\partial z_k}{\partial x_i} = \sum_k \cfrac{\partial J}{\partial z_k} \gamma_k \cfrac{\partial \hat{x}_k}{\partial x_i} \\ &=& \sum_k \cfrac{\partial J}{\partial z_k} \gamma_k \cfrac{1}{\sqrt{\sigma^2 + \varepsilon}} \left( \delta_{ki} - \cfrac{1}{N_f} - \cfrac{1}{N_f} \hat{x}_i \hat{x}_k \right) \\ &=& \cfrac{1}{\sqrt{\sigma^2 + \varepsilon}} \left( \sum_k \cfrac{\partial J}{\partial z_k} \gamma_k \delta_{ki} - \cfrac{1}{N_f} \sum_k \cfrac{\partial J}{\partial z_k} \gamma_k - \cfrac{1}{N_f} \sum_k \cfrac{\partial J}{\partial z_k} \gamma_k \hat{x}_i \hat{x}_k \right) \\ &=& \cfrac{1}{\sqrt{\sigma^2 + \varepsilon}} \left( \cfrac{\partial J}{\partial z_i} \gamma_i - \cfrac{1}{N_f} \sum_k \cfrac{\partial J}{\partial z_k} \gamma_k - \cfrac{1}{N_f} \hat{x}_i \sum_k \cfrac{\partial J}{\partial z_k} \gamma_k \hat{x}_k \right) \\ &=& \cfrac{1}{\sqrt{\sigma^2 + \varepsilon}} \left( g_i - \cfrac{1}{N_f} \sum_k g_k - \cfrac{1}{N_f} \hat{x}_i \sum_k g_k \hat{x}_k \right) \qquad \left( \boldsymbol{g} := \cfrac{\partial J}{\partial \boldsymbol{z}} \odot \boldsymbol{\gamma} \right) \end{eqnarray}\]

勾配クリッピング

RNN のような深いネットワークにおいて勾配爆発を防止する非常に有効な手法として、勾配クリッピング がある。

あるニューラルネットワークモデルを構成するの全ての層の学習パラメータの集合を $\boldsymbol{\theta}$ とする。コスト関数 $J$ の $\boldsymbol{\theta}$ による勾配ベクトル

\[\boldsymbol{g} := \cfrac{\partial J}{\partial \boldsymbol{\theta}}\]

に対して、そのノルム

\[\vert\vert \boldsymbol{g} \vert\vert = \sqrt{ \sum_k \left( \cfrac{\partial J}{\partial \theta_k} \right)^2 }\]

が閾値 $threshold$ を超えているとき、全ての勾配に $threshold\ /\ \vert\vert \boldsymbol{g} \vert\vert$ をかけて、勾配ベクトルの大きさが大きくなりすぎないように調整する：

\[\boldsymbol{g} \leftarrow \cfrac{threshold}{\vert\vert \boldsymbol{g} \vert\vert}\ \boldsymbol{g}\]

実装・動作確認

コード

MLP と共通のクラス

全結合層：

活性化関数：

SoftMax 関数：

損失関数（Cross-Entropy Loss）：

Batch Normalization：

Dropout：

RNN 独自のクラス

時系列データの分類器

動作確認

手作りデータセット1：周波数の異なる1次元サイン波

\[\begin{eqnarray} \mathrm{label\ 1}:\quad x(t) &=& \sin{f_1(t+t_\mathrm{random})} + noise \\ \\ \mathrm{label\ 2}:\quad x(t) &=& \sin{f_2(t+t_\mathrm{random})} + noise \\ \\ \mathrm{label\ 3}:\quad x(t) &=& \sin{f_3(t+t_\mathrm{random})} + noise \end{eqnarray}\]

の3種類の周波数 $f_1, f_2, f_3$ によってラベルが異なる1次元サイン波を様々な位相（$t_\mathrm{random}$）で生成して、RNN モデルで分類してみる。

学習データ生成：

N = 1200
N_train = int(N * 0.8)
N_test = N - N_train
#T = 16
T = 64

X, Y = RNNClassificationToyData().sin_multi_frequency(N, T)
X_train, Y_train = X[:N_train], Y[:N_train]
X_test, Y_test = X[N_train:], Y[N_train:]

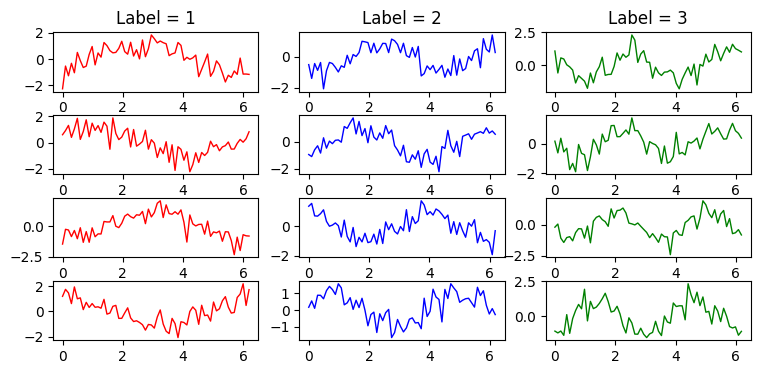
rnn_custom-data

モデル初期化・学習：

model_rnn = RNNClassifier(X_train, Y_train, X_test, Y_test,
    H_rnn=10, L_rnn=1, H_mlp=20, L_mlp=1,
    activation_func_rnn=HyperbolicTangent)
model_rnn.train(epoch=10000, mini_batch=80, eta=0.0005, log_interval=100)

# 学習曲線を描画
plt.figure(figsize=(9, 4))
plt.subplots_adjust(wspace=0.2, hspace=0.4)
plt.subplot(1, 2, 1)
model_rnn.plot_accuracy()
plt.subplot(1, 2, 2)
model_rnn.plot_loss()
plt.show()

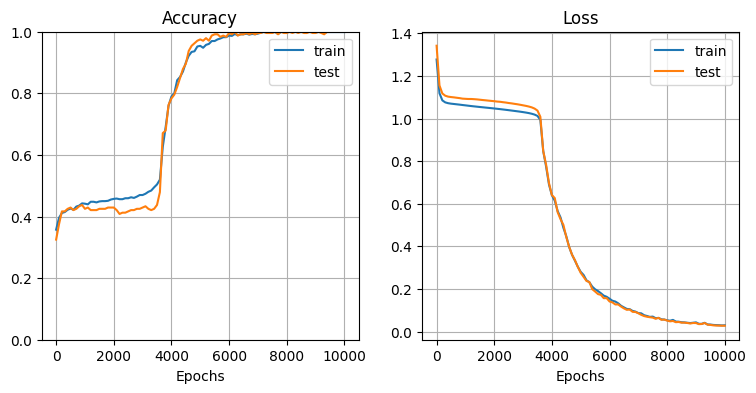
rnn_custom-data_learning-curve

→ ほぼ100%の精度で分類できている

手作りデータセット2：位相差のある2次元のサイン波

\[\begin{eqnarray} \mathrm{label\ 1}:\quad \begin{cases} x_1(t) &=& \sin{(t+t_\mathrm{random})} + noise \\ x_2(t) &=& \sin{(t+t_\mathrm{random}+\theta_1)} + noise \\ \end{cases} \\ \\ \mathrm{label\ 2}:\quad \begin{cases} x_1(t) &=& \sin{(t+t_\mathrm{random})} + noise \\ x_2(t) &=& \sin{(t+t_\mathrm{random}+\theta_2)} + noise \\ \end{cases} \\ \\ \mathrm{label\ 3}:\quad \begin{cases} x_1(t) &=& \sin{(t+t_\mathrm{random})} + noise \\ x_2(t) &=& \sin{(t+t_\mathrm{random}+\theta_3)} + noise \\ \end{cases} \end{eqnarray}\]

のように、2つのサイン波からなる2次元の時系列データを生成する。
2つの波の位相差 $\theta_1, \theta_2, \theta_3$ だけを変えて、分類できるか試してみる。

学習データ生成：

N = 1200
N_train = int(N * 0.8)
N_test = N - N_train
#T = 16
T = 64

X, Y = RNNClassificationToyData().sin_2d_multi_phase_diff(N, T)
X_train, Y_train = X[:N_train], Y[:N_train]
X_test, Y_test = X[N_train:], Y[N_train:]

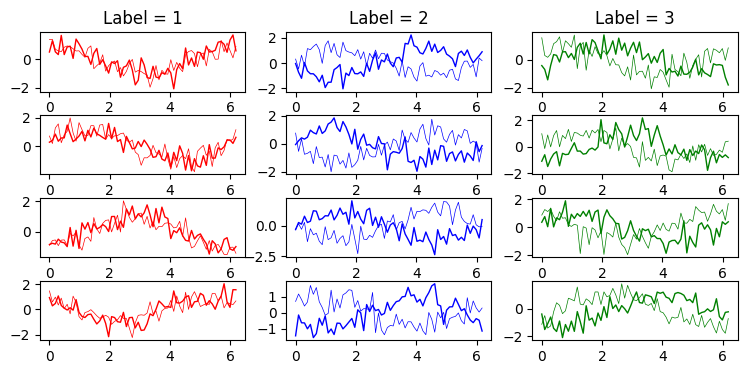
rnn_custom-data2

モデル初期化・学習：

model_rnn = RNNClassifier(X_train, Y_train, X_test, Y_test,
    H_rnn=10, L_rnn=1, H_mlp=20, L_mlp=1,
    activation_func_rnn=HyperbolicTangent)
model_rnn.train(epoch=5000, mini_batch=80, eta=0.0005, log_interval=100)

# 学習曲線を描画
plt.figure(figsize=(9, 4))
plt.subplots_adjust(wspace=0.2, hspace=0.4)
plt.subplot(1, 2, 1)
model_rnn.plot_accuracy()
plt.subplot(1, 2, 2)
model_rnn.plot_loss()
plt.show()

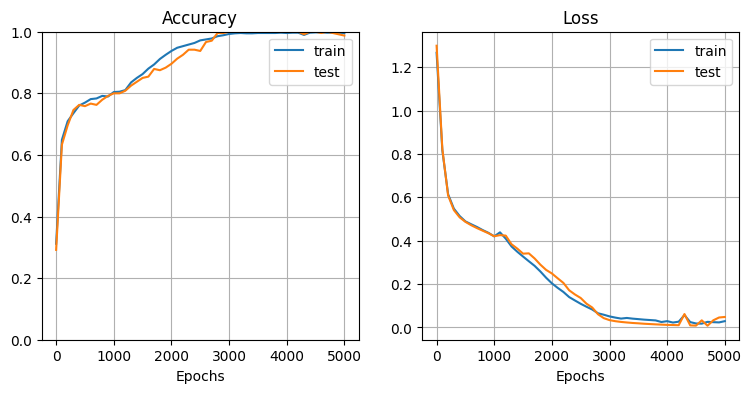
rnn_custom-data2_learning-curve

→ こちらもほぼ100%の精度で分類できている

MNIST 手書き数字画像

MNIST の手書き数字画像データ（$28\times 28$ ピクセル）を読み込み、

  • 各時刻の入力の特徴量が28個（28次元ベクトル）
  • 時系列長が28

の時系列データと見なして、many to one の分類問題を解いてみる。

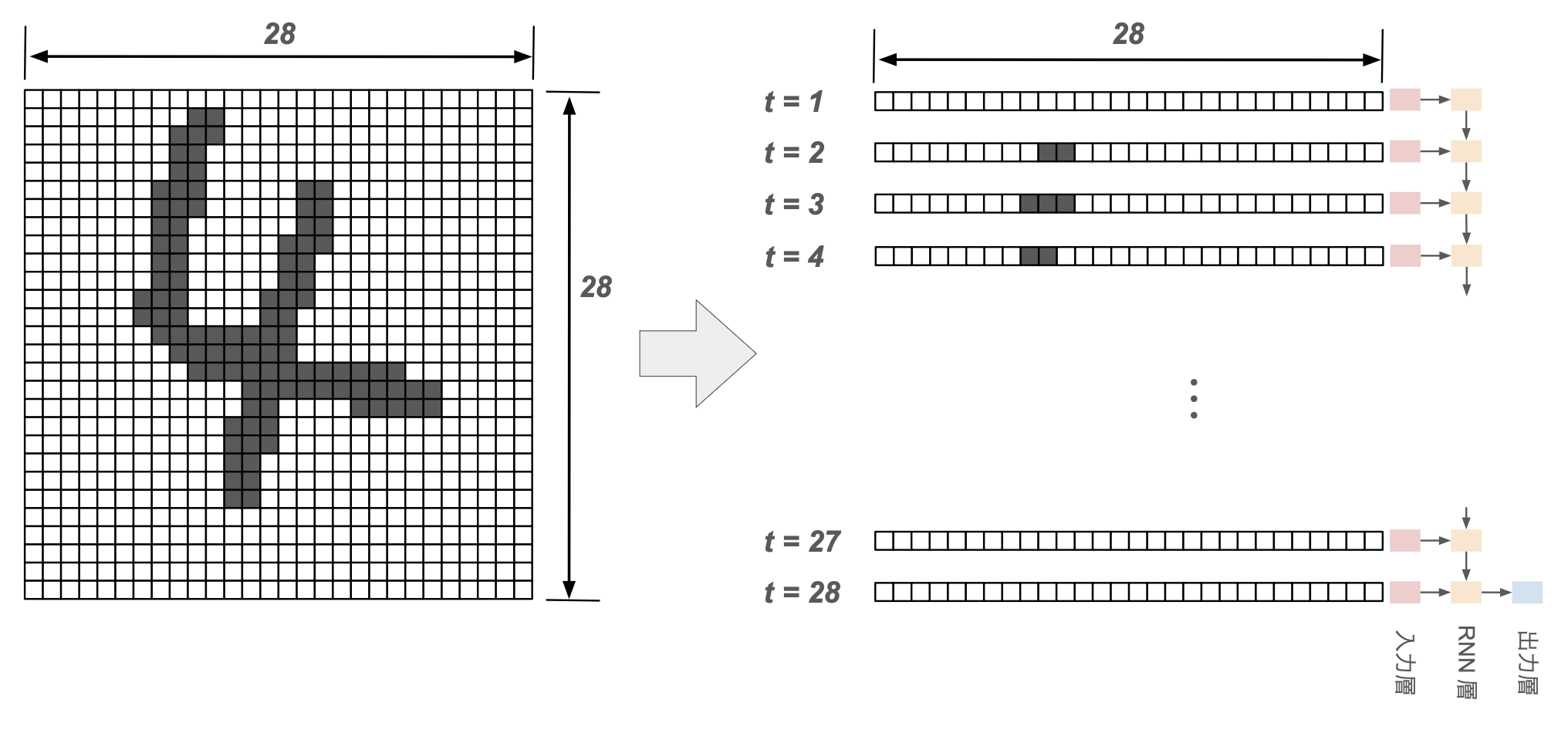
rnn_mnist-as-time-sequence

学習データ生成：

# 訓練データとテストデータを生成
X, Y = MnistClassificationData().rnn(10000)
X_test, Y_test = X[:1000], Y[:1000]
X_train, Y_train = X[1000:10000], Y[1000:10000]

モデル初期化・学習：

# モデル初期化・学習
model_rnn = RNNClassifier(X_train, Y_train, X_test, Y_test,
    H_rnn=10, L_rnn=1, H_mlp=20, L_mlp=1, activation_func_rnn=ReLU)
model_rnn.train(epoch=1000, mini_batch=10, eta=0.001, log_interval=5)

# 学習曲線を描画
plt.figure(figsize=(9, 4))
plt.subplots_adjust(wspace=0.2, hspace=0.4)
plt.subplot(1, 2, 1)
model_rnn.plot_precision()
plt.subplot(1, 2, 2)
model_rnn.plot_loss()
plt.show()

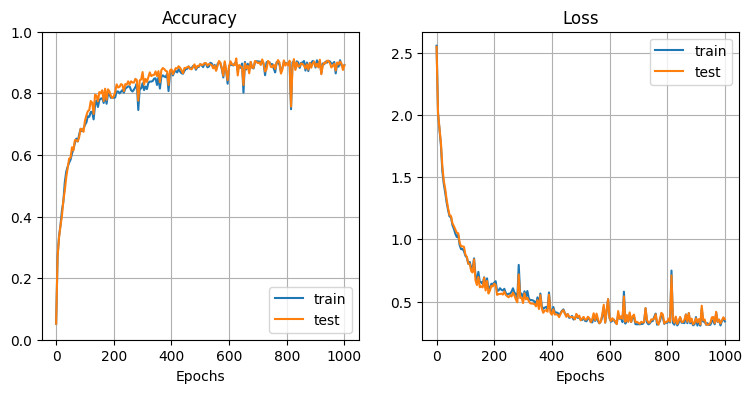
rnn_mnist_learning-curve

→ 最後の隠れ状態 $h_{28}$ だけを入力とした many to one のシンプルな RNN でも、80%以上の精度で手書き数字を分類できている。

【NOTE】

  • このデータセットの場合、各時系列のベクトルは多くの値がゼロ、特に $t=1$ 付近や $t=28$ 付近ではすべての値がゼロであることが多く、どんな重みに掛け算してもゼロになるので学習がやりにくいかも
  • Layer Normalization の導入についても、$t=0$ や $t=28$ 近く（余白）はすべてがゼロのベクトルとなり、標準化ができない（平均も標準偏差もゼロ）ため難しそう

他のハイパーパラメータはそのままで、RNN 層を2層に増やしてみる（L_rnn=2）：

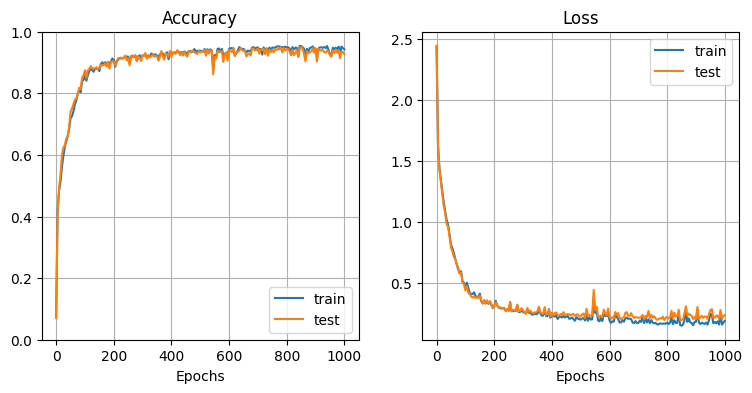
rnn_mnist_2layers_learning-curve

→ モデルの表現力が上がり、Precision が向上。

実験・調査

勾配クリッピングの有無

前述の手作りデータセット2（位相差の異なる2次元サイン波）について、勾配クリッピングを外して比較してみる。

model_rnn = RNNClassifier(X_train, Y_train, X_test, Y_test,
    H_rnn=10, L_rnn=1, H_mlp=20, L_mlp=1, activation_func_rnn=HyperbolicTangent)
model_rnn.train(epoch=5000, mini_batch=80, eta=0.0005, log_interval=100)

rnn_custom-data2_learning-curve

勾配クリッピングを外す：

model_rnn = RNNClassifier(X_train, Y_train, X_test, Y_test,
    H_rnn=10, L_rnn=1, H_mlp=20, L_mlp=1, activation_func_rnn=HyperbolicTangent)
model_rnn.train(epoch=5000, mini_batch=80, eta=0.0001, log_interval=100)

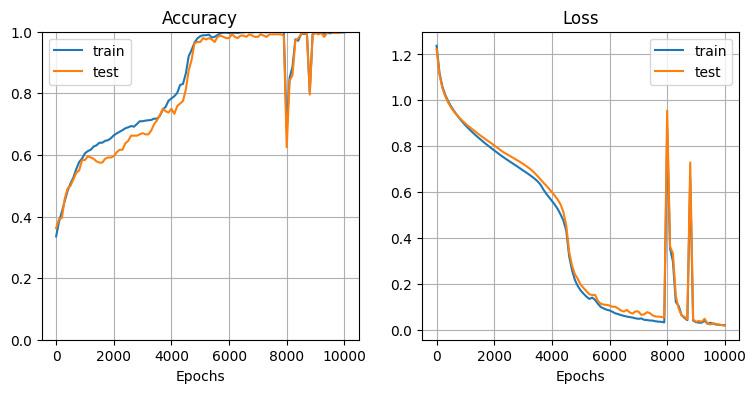
rnn_custom-data2_learning-curve_noclip

学習率 $\eta = 0.0005$ では大きすぎて学習が安定せず、$\eta = 0.0001$ で比較的安定するようになった。
それでもまだ不安定な箇所が見られ、勾配クリッピングの有効性が確認できた。