多層パーセプトロン(MLP)とは
MLP = Multi-Layer Perceptron
全ての入力(総入力)を受けて1つの出力値を計算・出力する単一ニューロンを多数組み合わせて、複雑な関数のモデリングを可能とする技術。
ニューラルネットワークの1種。
概観
下図に MLP の概観を示す。
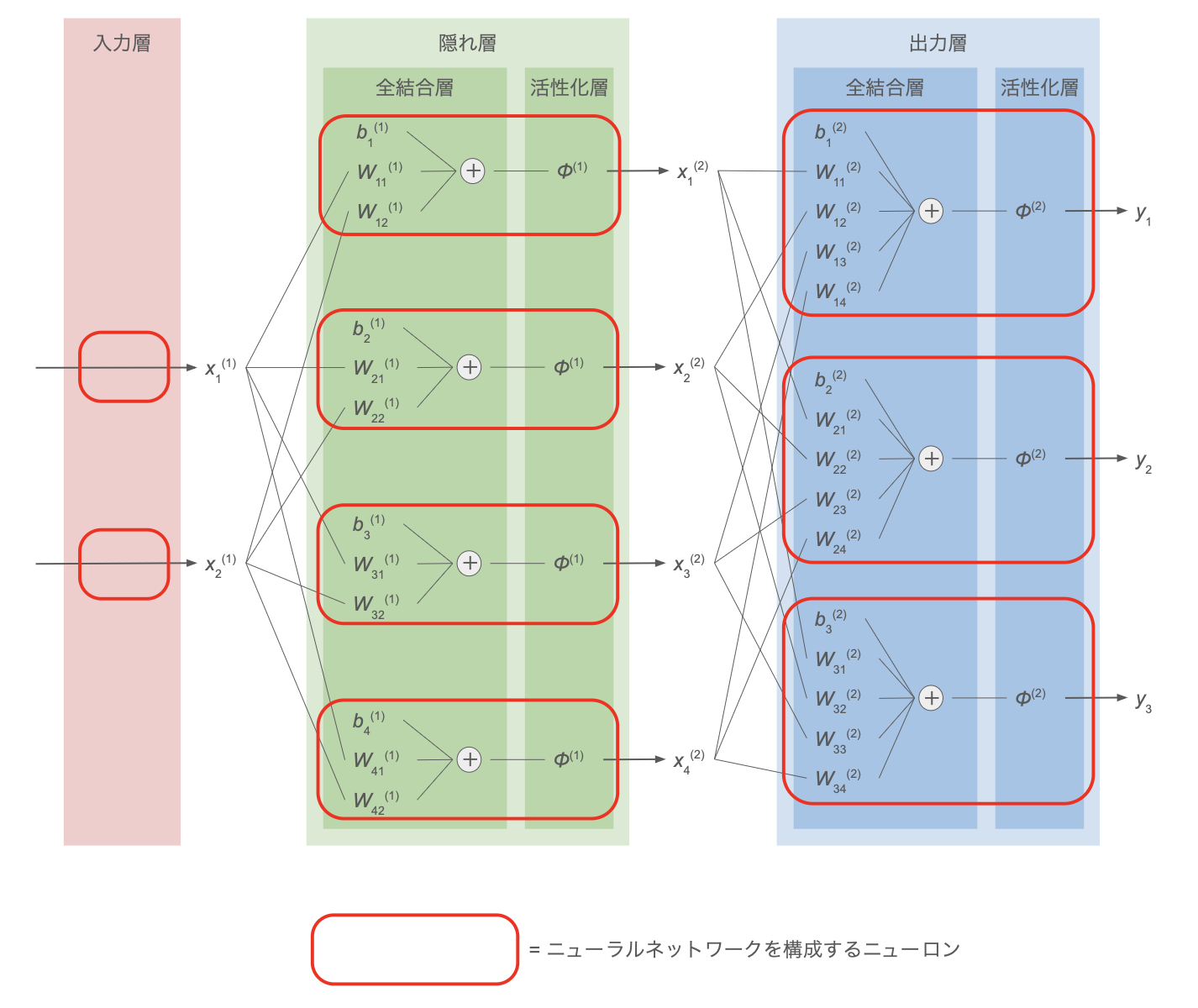
| 処理層 | 説明 |
|---|---|
| 入力層 | 生の入力データに相当する層 |
| 出力層 | モデルの最終的な出力に相当する層 |
| 隠れ層 | 入力層と出力層の間の中間データに相当する層。 出力層から得られる最終出力値と違い、計算途中の中間データであるため直接には値が見えない(= 隠れている)ためこう呼ばれるが、処理の内容(後述)は出力層と同じ |
| 全結合層 | 前層の各出力値に重みをかけ、バイアス項を加えて和を取る層 |
| 活性化層 | 全結合層の出力値に何らかの活性化関数を適用する層 |
隠れ層は、図のように1つである必要はなく、複数の隠れ層でニューロン数が異なっていても良い。
隠れ層が多く、各層が持つニューロンが多いほど複雑なモデルを表現できる。
上図では、
- 隠れ層の数:1つ
- 各層のニューロン数
- 入力層:2つ
- 隠れ層:4つ
- 出力層:3つ
全結合層の処理
隠れ層・出力層の前半である 全結合層 の各ニューロンでは、1つ前の層の全ての出力に重みをかけたものにバイアス項を加えた
\[a_i^{(l)} := \displaystyle \sum_k W_{ik}^{(l)} x_k^{(l)} + b_i^{(l)} \tag{1}\]を計算する。
活性化層の処理
後半の 活性化層 では、この $a_i^{(l)}$ を 総入力 として、これにシグモイド関数や ReLU などの活性化関数を適用した値
\[x_i^{(l+1)} = \phi^{(l)} \left( a_i^{(l)} \right) = \phi^{(l)} \left( \displaystyle \sum_k W_{ik}^{(l)} x_k^{(l)} + b_i^{(l)} \right) \tag{2}\]を出力とする。
以上の式は、行列・ベクトルを用いて以下のようにも記述できる。
\[\boldsymbol{a}^{(l)} := W^{(l)} \boldsymbol{x}^{(l)} + \boldsymbol{b}^{(l)} \tag{1'}\] \[\boldsymbol{x}^{(l+1)} = \phi^{(l)} \left( \boldsymbol{a}^{(l)} \right) = \phi^{(l)} \left( W^{(l)} \boldsymbol{x}^{(l)} + \boldsymbol{b}^{(l)} \right) \tag{2'}\]ただし、
\[W^{(l)} = \begin{pmatrix} w_{11}^{(l)} & \cdots & w_{1m}^{(l)} \\ \vdots & & \vdots \\ w_{t1}^{(l)} & \cdots & w_{tm}^{(l)} \end{pmatrix}\] \[\boldsymbol{b}^{(l)} = \begin{pmatrix} b_1^{(l)} \\ \vdots \\ b_t^{(l)} \\ \end{pmatrix}\] \[\boldsymbol{x}^{(l)} = \begin{pmatrix} x_1^{(l)} \\ \vdots \\ \vdots \\ x_m^{(l)} \\ \end{pmatrix}, \qquad \boldsymbol{x}^{(l+1)} = \begin{pmatrix} x_1^{(l+1)} \\ \vdots \\ x_t^{(l+1)} \\ \end{pmatrix}\]MLP では、以上のように $\boldsymbol{x}^{(l)}$ から $\boldsymbol{x}^{(l+1)}$ を計算する処理を複数回繰り返すことで最終出力
\[\boldsymbol{y} := \begin{pmatrix} y_1 \\ \vdots \\ y_n \\ \end{pmatrix}\]を得る。
MLP の学習段階では、コスト関数を最小化する(あるいは評価関数を最大化する)最適な $W_{ik}^{(l)}, b_i^{(l)}$ を学習する。
学習の流れ
MLP の学習の流れは以下の通り。
- 【0】ランダムな値でパラメータ $W_{ik}^{(l)}, b_i^{(l)}$ を初期化
- 【1】順伝播による出力・コスト関数計算:入力層から出力層へ向かって順次ニューロンの計算を進め、入力 $\boldsymbol{x}$ に対して最終層の出力 $\boldsymbol{y}$ を得てコスト関数 $J(\boldsymbol{y})$ を計算
- 【2】コスト関数の 誤差逆伝播 による重み更新:コスト関数の勾配(誤差)を計算して、重みを更新
- 【3】収束条件を満たすまで1〜2を繰り返す
1. 順伝播による出力・コスト関数計算
- 前述の式 $(1) (2)$ を用いて、前層の出力 $\boldsymbol{x}^{(l)}$ から次の層の出力 $\boldsymbol{x}^{(l+1)}$ を計算する作業を繰り返して最終的な出力 $\boldsymbol{y}$ を得る
- 最終的な出力値に対するコスト関数 $J(\boldsymbol{y})$ を計算
2. コスト関数の誤差逆伝播(バックプロパゲーション)による重み更新
勾配降下法により各パラメータ $W_{ik}^{(l)}, b_i^{(l)}$ を改善するため、これらのパラメータによるコスト関数 $J$ の偏微分
\[\cfrac{\partial J}{\partial W_{ij}}, \quad \cfrac{\partial J}{\partial b_{i}}\]を計算したい。
基礎理論
ネットワークを構成する層の1つ(全結合層でも活性化層でも何でも OK)に注目して考える。
この層について、
- $\boldsymbol{x}_\mathrm{in}$:この層への入力(= 前層からの出力)
- $\boldsymbol{x}_\mathrm{out}$:この層からの出力
- $\boldsymbol{p}$:入力 $\boldsymbol{x}\mathrm{in}$ から出力 $\boldsymbol{x}\mathrm{out}$ を計算するためのこの層内のパラメータ
- $\boldsymbol{q}$:この層より後の層に含まれる全てのパラメータの集合
とする。
【NOTE】
例えば、$l$ 番目の全結合層であれば
- $\boldsymbol{x}_\mathrm{in} = (x_1^{(l)}, x_2^{(l)}, \cdots)$
- $\boldsymbol{x}_\mathrm{out} = (x_1^{(l+1)}, x_2^{(l+1)}, \cdots)$
- $\boldsymbol{p} = (W^{(l)}, \boldsymbol{b}^{(l)})$
- $\boldsymbol{q} = (W^{(l+1)}, W^{(l+2)}, \cdots, \boldsymbol{b}^{(l+1)}, \boldsymbol{b}^{(l+2)}, \cdots)$
$\boldsymbol{p}$ の成分 $p_1, p_2, \cdots$(= 学習により最適化したいパラメータ)によるコスト関数 $J$ の偏微分
\[\cfrac{\partial J}{\partial p_i}\]を考えたい。
出力 \(\boldsymbol{x}_\mathrm{out}\) は入力 \(\boldsymbol{x}_\mathrm{in}\) と層内パラメータ \(\boldsymbol{p}\) から計算されるので、これらを独立変数とする関数とみなせる:
\[\boldsymbol{x}_\mathrm{out} = \boldsymbol{x}_\mathrm{out} (\boldsymbol{x}_\mathrm{in}, \boldsymbol{p})\](((ToDo: 説明画像)))
また、コスト関数 $J$ の計算には最終出力 $\boldsymbol{y}$ を使うが、これは $\boldsymbol{x}_\mathrm{out}$ とこれより後の層のパラメータ $\boldsymbol{q}$ から計算できる。したがって、$J$ はこれらを独立変数とする関数とみなせる:
\[J = J (\boldsymbol{x}_\mathrm{out}, \boldsymbol{q}) = J (\boldsymbol{x}_\mathrm{out}(\boldsymbol{x}_\mathrm{in}, \boldsymbol{p}), \boldsymbol{q})\](((ToDo: 説明画像)))
$\boldsymbol{x}_\mathrm{in}, \boldsymbol{p}, \boldsymbol{q}$ はそれぞれ独立であるから、偏微分の性質より
\[\cfrac{\partial J}{\partial p_i} = \displaystyle \sum_k \cfrac{\partial J}{\partial x_{\mathrm{out},k}(\boldsymbol{x}_\mathrm{in}, \boldsymbol{p})} \cfrac{\partial x_{\mathrm{out},k}(\boldsymbol{x}_\mathrm{in}, \boldsymbol{p})}{\partial p_i} \tag{3}\] \[\cfrac{\partial J}{\partial x_{\mathrm{in},i}} = \displaystyle \sum_k \cfrac{\partial J}{\partial x_{\mathrm{out},k}(\boldsymbol{x}_\mathrm{in}, \boldsymbol{p})} \cfrac{\partial x_{\mathrm{out},k}(\boldsymbol{x}_\mathrm{in}, \boldsymbol{p})}{\partial x_{\mathrm{in},i}} \tag{4}\]それぞれの式の後半の偏微分
\(\cfrac{\partial x_{\mathrm{out},k}(\boldsymbol{x}_\mathrm{in}, \boldsymbol{p})}{\partial p_i},\ \ \cfrac{\partial x_{\mathrm{out},k}(\boldsymbol{x}_\mathrm{in}, \boldsymbol{p})}{\partial x_{\mathrm{in},i}}\) は、この層で行う処理の定義($\boldsymbol{x}_\mathrm{out}$ の計算式)から解析的に計算できる。
一方、前半の偏微分 \(\cfrac{\partial J}{\partial x_{\mathrm{out},k}(\boldsymbol{x}_\mathrm{in}, \boldsymbol{p})}\) は直接計算できないが、これは1つ後ろの層に注目して考えたときの入力による微分 \(\cfrac{\partial J}{\partial x_{\mathrm{in},k}}\) に一致する。
したがって、1つ後ろの層の微分が分かれば前の層の微分が全て計算できる。
また、コスト関数 $J$ は最終層(出力層)の出力値 $\boldsymbol{y}$ のみで定義・計算される関数であるから、最終層の変数による $J$ の微分は解析的な計算で求められる。
したがって、出力層の微分から出発して入力層に向かって再帰的に微分(誤差)を計算していき、全ての層の微分を求めることができる(誤差逆伝播法)。
各層におけるコスト関数の勾配
各層のパラメータについて、コスト関数の勾配を計算する。
全結合層
入力変数
| 変数 | 説明 |
|---|---|
| $\boldsymbol{x}$ | 前層の出力 |
| $W$ | $\boldsymbol{x}$ に付加する重み |
| $\boldsymbol{b}$ | バイアス項 |
出力変数
\[z_i := \displaystyle \sum_k W_{ik} x_k + b_i\] \[\boldsymbol{z} := W \boldsymbol{x} + \boldsymbol{b}\]勾配の導出
\[\cfrac{\partial z_i}{\partial x_j} = W_{ij},\quad \cfrac{\partial z_i}{\partial b_i} = 1,\quad \cfrac{\partial z_i}{\partial W_{jk}} = \begin{cases} x_k & \rm{\quad if \quad} i = j \\ 0 & \rm{\quad if \quad} i \neq j \end{cases}\]より、
\[\begin{eqnarray} \cfrac{\partial J}{\partial x_i} &=& \displaystyle \sum_k \cfrac{\partial J}{\partial z_k} \cfrac{\partial z_k}{\partial x_i} = \displaystyle \sum_k \cfrac{\partial J}{\partial z_k} W_{ki} = \displaystyle \sum_k W_{ik}^T \cfrac{\partial J}{\partial z_k} = \left( W^T \cfrac{\partial J}{\partial \boldsymbol{z}} \right)_i \\ \cfrac{\partial J}{\partial W_{ij}} &=& \displaystyle \sum_k \cfrac{\partial J}{\partial z_k} \cfrac{\partial z_k}{\partial W_{ij}} = \cfrac{\partial J}{\partial z_i} \cfrac{\partial z_i}{\partial W_{ij}} = \cfrac{\partial J}{\partial z_i} x_j = \left( \cfrac{\partial J}{\partial \boldsymbol{z}} \boldsymbol{x}^T \right)_{ij} \\ \cfrac{\partial J}{\partial b_i} &=& \displaystyle \sum_k \cfrac{\partial J}{\partial z_k} \cfrac{\partial z_k}{\partial b_i} = \cfrac{\partial J}{\partial z_i} \cfrac{\partial z_i}{\partial b_i} = \cfrac{\partial J}{\partial z_i} = \left( \cfrac{\partial J}{\partial \boldsymbol{z}} \right)_i \end{eqnarray}\]活性化層
入力変数
| 変数 | 説明 |
|---|---|
| $\boldsymbol{x}$ | 前層の出力 |
出力変数
\[\boldsymbol{z} = \phi \left( \boldsymbol{x} \right)\]勾配の導出
\[\cfrac{\partial J}{\partial x_i} = \displaystyle \sum_k \cfrac{\partial J}{\partial z_k} \cfrac{\partial z_k}{\partial x_i} = \displaystyle \sum_k \cfrac{\partial J}{\partial z_k} \cfrac{\partial \phi \left( \boldsymbol{x} \right)_k}{\partial x_i}\]主な活性化関数 $\phi$ とその微分 $\partial \phi / \partial x_i$ については後述。
SoftMax 層
入力変数
| 変数 | 説明 |
|---|---|
| $\boldsymbol{x}$ | 前層の出力 |
出力変数
\[z_i = \cfrac{e^{x_i}}{\sum_k e^{x_k}}\]勾配の導出
\[\begin{eqnarray} \cfrac{\partial J}{\partial x_i} &=& \displaystyle \sum_k \cfrac{\partial J}{\partial z_k} \cfrac{\partial z_k}{\partial x_i} \\ &=& \displaystyle \sum_k \cfrac{\partial J}{\partial z_k} \cfrac{\frac{\partial e^{x_k}}{\partial x_i} \sum_l e^{x_l} - \frac{\partial \left(\sum_l e^{x_l}\right)}{\partial x_i} e^{x_k}} { \left(\sum_l e^{x_l}\right)^2 } \\ &=& \displaystyle \sum_k \cfrac{\partial J}{\partial z_k} \cfrac{ \delta_{ki} e^{x_i} \sum_l e^{x_l} - e^{x_i} e^{x_k} } { \left(\sum_l e^{x_l}\right)^2 } \\ &=& \displaystyle \sum_k \cfrac{\partial J}{\partial z_k} \left(\delta_{ki} z_i - z_i z_k\right) \\ &=& z_i \left( \cfrac{\partial J}{\partial z_i} - \sum_k \cfrac{\partial J}{\partial z_k} z_k \right) \end{eqnarray}\]ただし、$\delta_{ki}$ はクロネッカーのデルタ($k=i$ のときのみ1、他は0)を表す。
最終出力に対するコスト関数の勾配
分類問題において対数尤度を用いる場合を想定して、最終出力 $\boldsymbol{y}$ についてのコスト関数の勾配を計算する。
入力変数
| 変数 | 説明 |
|---|---|
| $\hat{\boldsymbol{y}}^{(k)}$ | 前層の出力のうち、ミニバッチの $k$ 番目のサンプル。 ソフトマックス層などで計算された、サンプルが各ラベルへ所属する確率のベクトル |
| $\boldsymbol{y}^{(k)}$ | ミニバッチの $k$ 番目のサンプルの正解クラスラベルを表す確率のベクトル。正解クラスに対応する成分のみ1、他成分は0 |
出力変数
出力はコスト関数 $J$。
ロジスティック回帰と同様に、与えられた教師データが実現する尤度(対数尤度)を最大化する場合を考える。
このとき、コスト関数 $J$ は対数尤度にマイナスをかけたものとなる:
勾配の導出
\[\begin{eqnarray} \cfrac{\partial J}{\partial \hat{y_j^{(i)}}} &=& - \left( \cfrac{y_j^{(i)}}{\hat{y_j^{(i)}}} - \cfrac{1-y_j^{(i)}}{1-\hat{y_j^{(i)}}} \right) \\ &=& \cfrac{\hat{y_j^{(i)}} - y_j^{(i)}}{\hat{y_j^{(i)}} \left(1-\hat{y_j^{(i)}}\right) } \end{eqnarray}\]重みの更新
以上により、全ての重みに関するコスト関数の勾配が求まるので、
\[W_{ij}^{(l)} \longleftarrow W_{ij}^{(l)} - \eta \cfrac{\partial J(W, \boldsymbol{b})}{\partial W_{ij}^{(l)}}\] \[b_i^{(l)} \longleftarrow W_i^{(l)} - \eta \cfrac{\partial J(W, \boldsymbol{b})}{\partial b_i^{(l)}}\]によりパラメータを更新する。
$\eta$ は学習率。
また、L2 正則化を行う場合は正則化項の微分
\[\cfrac{\partial}{\partial W_{ij}^{(l)}} \left( \cfrac{\lambda}{2} \displaystyle \sum_{i^{'}} \sum_{j^{'}} \sum_{l^{'}} \left(W_{i^{'}j^{'}}^{(l^{'})}\right)^2 \right) = \lambda W_{ij}^{(l)}\]をコスト関数の勾配に加える。
主な活性化関数

シグモイド関数(ロジスティック関数)
\[\phi(x_j) := \cfrac{1}{1 + e^{-x_j}}\] \[\cfrac{\partial \phi(x_j)}{\partial x_i} = \begin{cases} \cfrac{e^{-x_j}}{(1 + e^{-x_j})^2} = \phi(x_j)\left(1-\phi(x_j)\right) \quad &(i = j) \\ \\ 0 \quad &(i\ne j) \end{cases}\]双曲線正接関数(ハイパボリックタンジェント)
\[\phi(z_j) := \tanh(z_j) = \cfrac{e^{z_j} - e^{-z_j}}{e^{z_j} + e^{-z_j}}\] \[\cfrac{\partial \phi(x_j)}{\partial x_i} = \begin{cases} \cfrac{1}{\cosh^2 (z_j)} = \cfrac{4}{\left(e^{z_j} + e^{-z_j}\right)^2} \quad &(i = j) \\ \\ 0 \quad &(i\ne j) \end{cases}\]ReLU 関数(Rectified Linear Unit)
\[\phi(x_j) := \begin{cases} 0 & (x_j \le 0) \\ x_j & (x_j \gt 0) \end{cases}\] \[\cfrac{\partial \phi(x_j)}{\partial x_i} = \begin{cases} 0 & (\mathrm{}x_j \le 0 \ \ \mathrm{or}\ \ i\ne j) \\ 1 & (x_j \gt 0 \ \ \mathrm{and}\ \ i=j) \end{cases}\]SoftMax 関数
\[\phi(z_j) = \cfrac{e^{z_j}}{\displaystyle \sum_k e^{z_k}}\] \[\cfrac{\partial \phi(z_i)}{\partial z_j} = \begin{cases} \cfrac{e^{z_j} \sum_k e^{z_k} - (e^{z_j})^2}{\left(\sum_k e^{z_k}\right)^2} &=& \phi(z_j) \left( 1 - \phi(z_j) \right) &\quad (i = j) \\ \\ - \cfrac{e^{z_j} e^{z_i}}{\left(\sum_k e^{z_k}\right)^2} &=& - \phi(z_i) \phi(z_j) &\quad (i \neq j) \end{cases}\]全ての $j$ で和を取ると1になることから、分類問題における各ラベルへの所属確率として、出力層の活性化関数に使うことが多い。
【NOTE】活性化関数には非線形関数を使う
隠れ層が1つであるような MLP を考え、仮に活性化関数 $\phi$ が線形関数であるとする。
\[\phi(z) := cz + b \ (c, b = const.)\]隠れ層の出力値は、
\[a_j^{(1)} = \phi \left(z_j^{(1)}\right) = c \sum_i W_{ji}^{(1)} a_i + b\]出力層の出力値は、
\[\begin{eqnarray} a_j^{(2)} &=& \phi \left(z_j^{(2)}\right) \\ &=& c \displaystyle \sum_i W_{ji}^{(2)} a_i^{(1)} + b \\ &=& c \displaystyle \sum_i W_{ji}^{(2)} \left( c\left(\sum_k W_{ik}^{(1)} x_k\right) + b \right) + b \\ &=& c^2 \displaystyle \sum_k \sum_i W_{ik}^{(1)} W_{ji}^{(2)} x_k + b\left( 1 + c \sum_i W_{ji}^{(2)} \right) \end{eqnarray}\]これは結局 $x_i$ の一次式であり、入力値を一度線形変換したものに過ぎない。
つまり隠れ層なしでも同じ計算を実現でき、層を深くすることによる恩恵が得られない。
改善のための手法
Batch Normalization
ミニバッチ学習(各ステップで、学習データ全てではなく一部をランダムに抽出したものを使う)において、活性化関数の適用前にミニバッチ内で正規化(標準化)の処理を行う層を挟むことで、重みが大きくなりすぎて過学習が起こるのを防ぐ。
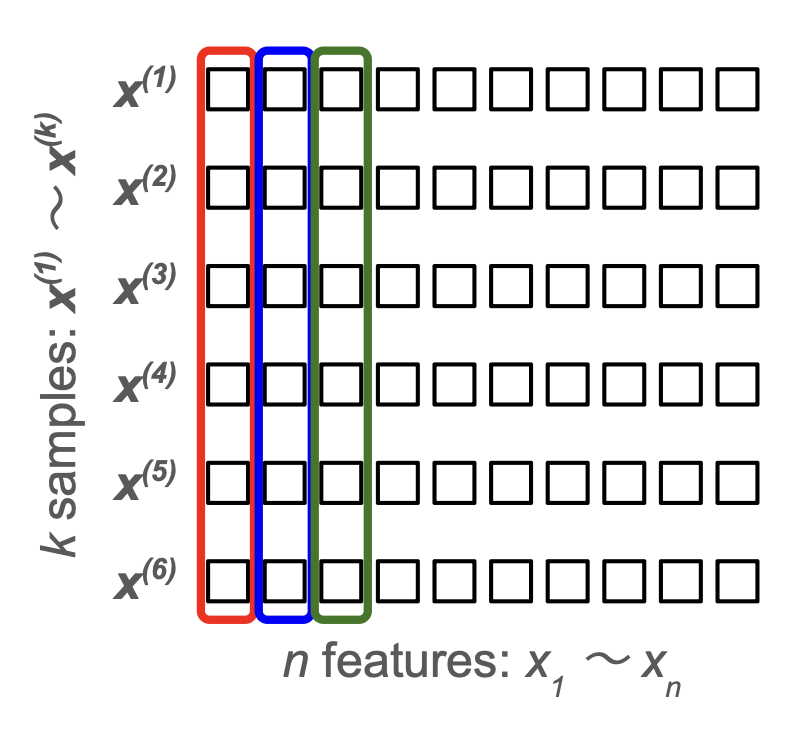
- 学習時:全結合層の出力を各特徴量ごとに標準化した後、パラメータでスケール & シフトしてから活性化層に渡す(後述)
- 推論時:学習中にミニバッチごとに平均と標準偏差の移動平均を更新していき、それを適用して標準化する
- $\mu \leftarrow (1-\alpha) \mu + \alpha \mu_\mathrm{batch}$
- $\sigma^2 \leftarrow (1-\alpha) \sigma^2 + \alpha \sigma_\mathrm{batch}^2$
- ただし、$0 \lt \alpha \lt 1$ は移動平均のモメンタムと呼ばれるパラメータで、$0.1$ や $0.01$ 程度の値がよく用いられる
【NOTE】推論時に移動平均を使う理由
学習の完了後、実際に推論を行う際には、バッチサイズが1であることが多く、平均や標準偏差といった統計量が意味を為さない。
そのため、学習中にデータサンプルの母集団の平均・標準偏差を求めておいてそれを使う。
入力変数
| 変数 | 説明 |
|---|---|
| $\boldsymbol{x}^{(k)}$ | 前層の出力のうち、ミニバッチの $k$ 番目のサンプル |
| $\boldsymbol{\gamma}$ | $\boldsymbol{x}^{(k)}$ と同じ次元の調整用変数(重み) |
| $\boldsymbol{\beta}$ | $\boldsymbol{x}^{(k)}$ と同じ次元の調整用変数(バイアス) |
| $N$ | ミニバッチのサイズ(サンプル数)→ 定数 |
中間変数
| 変数 | 説明 |
|---|---|
| $\boldsymbol{\mu}$ | $\boldsymbol{x}$ のミニバッチ内平均 |
| $\boldsymbol{\sigma}$ | $\boldsymbol{x}$ のミニバッチ内標準偏差 |
| $\hat{\boldsymbol{x}}^{(k)}$ | $\boldsymbol{x}^{(k)}$ をミニバッチ内で標準化したもの |
※ ベクトルの2乗は各成分を2乗している(アダマール積)
※ $\varepsilon$ は $10^{-14}$ などゼロ除算を防ぐための非常に小さい正の数
出力変数
\[\boldsymbol{z}^{(k)} = \boldsymbol{\gamma} \odot \hat{\boldsymbol{x}}^{(k)} + \boldsymbol{\beta}\]$\odot$ は同じ成分同士の積を取る演算(アダマール積)を表す。
勾配の導出
\[\cfrac{\partial \mu_i}{\partial x_i^{(j)}} = \cfrac{1}{N}\] \[\cfrac{\partial \sigma_i^2}{\partial x_i^{(j)}} = \cfrac{2}{N} \left( x_i^{(j)} - \mu_i \right)\]より、
\[\begin{eqnarray} \cfrac{\partial J}{\partial \gamma_i} &=& \displaystyle \sum_k \cfrac{\partial J}{\partial z_i^{(k)}} \cfrac{\partial z_i^{(k)}}{\partial \gamma_i} = \displaystyle \sum_k \cfrac{\partial J}{\partial z_i^{(k)}} \hat{x}_i^{(k)} \\ \\ \cfrac{\partial J}{\partial \beta_i} &=& \displaystyle \sum_k \cfrac{\partial J}{\partial z_i^{(k)}} \cfrac{\partial z_i^{(k)}}{\partial \beta_i} = \displaystyle \sum_k \cfrac{\partial J}{\partial z_i^{(k)}} \\ \\ \cfrac{\partial J}{\partial x_i^{(j)}} &=& \displaystyle \sum_k \cfrac{\partial J}{\partial z_i^{(k)}} \cfrac{\partial z_i^{(k)}}{\partial x_i^{(j)}} = \displaystyle \sum_k \cfrac{\partial J}{\partial z_i^{(k)}} \cfrac{\partial z_i^{(k)} \left( x_i, \mu_i(x_i), \sigma_i^2(x_i) \right) }{\partial x_i^{(j)}} \\ &=& \displaystyle \sum_k \cfrac{\partial J}{\partial z_i^{(k)}} \gamma_i \left( \cfrac{1}{\sqrt{\sigma_i^2 + \varepsilon}} \delta_{jk} - \cfrac{\partial \mu_i}{\partial x_i^{(j)}} \cfrac{1}{\sqrt{\sigma_i^2 + \varepsilon}} - \cfrac{\partial \sigma_i^2}{\partial x_i^{(j)}} \cfrac{x_i^{(k)} - \mu_i}{2 \left( \sqrt{\sigma_i^2 + \varepsilon} \right)^3} \right) \\ &=& \displaystyle \sum_k \cfrac{\partial J}{\partial z_i^{(k)}} \gamma_i \left( \cfrac{1}{\sqrt{\sigma_i^2 + \varepsilon}} \delta_{jk} - \cfrac{1}{N} \cfrac{1}{\sqrt{\sigma_i^2 + \varepsilon}} - \cfrac{1}{N} \left( x_i^{(j)} - \mu_i \right) \cfrac{x_i^{(k)} - \mu_i}{\left( \sqrt{\sigma_i^2 + \varepsilon} \right)^3} \right) \\ &=& \cfrac{\gamma_i}{N \sqrt{\sigma_i^2 + \varepsilon}} \left( N \cfrac{\partial J}{\partial z_i^{(j)}} - \displaystyle \sum_k \cfrac{\partial J}{\partial z_i^{(k)}} - \hat{x}_i^{(j)} \displaystyle \sum_k \cfrac{\partial J}{\partial z_i^{(k)}} \hat{x}_i^{(k)} \right) \\ &=& \cfrac{\gamma_i}{N \sqrt{\sigma_i^2 + \varepsilon}} \left( N \cfrac{\partial J}{\partial z_i^{(j)}} - \displaystyle \cfrac{\partial J}{\partial \beta_i} - \hat{x}_i^{(j)} \cfrac{\partial J}{\partial \gamma_i} \right) \\ &=& \left\{ \cfrac{1}{N} \cfrac{\boldsymbol{\gamma}}{\sqrt{\boldsymbol{\sigma}^2 + \varepsilon}} \odot \left( N \cfrac{\partial J}{\partial \boldsymbol{z}^{(j)}} - \displaystyle \cfrac{\partial J}{\partial \boldsymbol{\beta}} - \hat{\boldsymbol{x}}^{(j)} \odot \cfrac{\partial J}{\partial \boldsymbol{\gamma}} \right) \right\}_i \\ \end{eqnarray}\]Dropout
全結合層の重みについて、過学習を防ぐための手法の1つ。
- 学習時:各学習ステップごとに隠れ層内のニューロンを一定割合($0 \lt r_\mathrm{drop} \lt 1$)でランダムに選択し、このステップでは、そのニューロンの情報を後ろの層に伝達させない。誤差逆伝播の際にも、無効化したニューロンの重みは更新しない
- 推論時:全てのニューロンを利用して計算を行うが、隠れ層の結果に $1-r_\mathrm{drop}$ を掛け算してから次の隠れ層・出力層へ渡す(学習時と同じスケールにする)

Skip Connection (Residual Connection)
スキップ接続(残差接続)。ResNet (2015) で提案された手法。
この論文は CNN での検証だが、単純な多層パーセプトロンや RNN などいろいろなニューラルネットワークに適用できる。
ニューラルネットワークの層が深くなっていくと、勾配消失の問題に直面する。
これを回避するため、下図のようにネットワークを迂回する形で浅い層の値をそのまま伝える経路を取り、深い層の出力に加算する。
層を通過することでデータの次元が変わる場合は、行列による線形変換(CNN でチャンネル数が変わる場合は $1\times 1$ の畳み込み層)で次元を揃えてから加算する方法が主流:
\[\boldsymbol{x}^{(k+n)} \leftarrow \boldsymbol{x}^{(k+n)} + W \boldsymbol{x}^{(k)}\]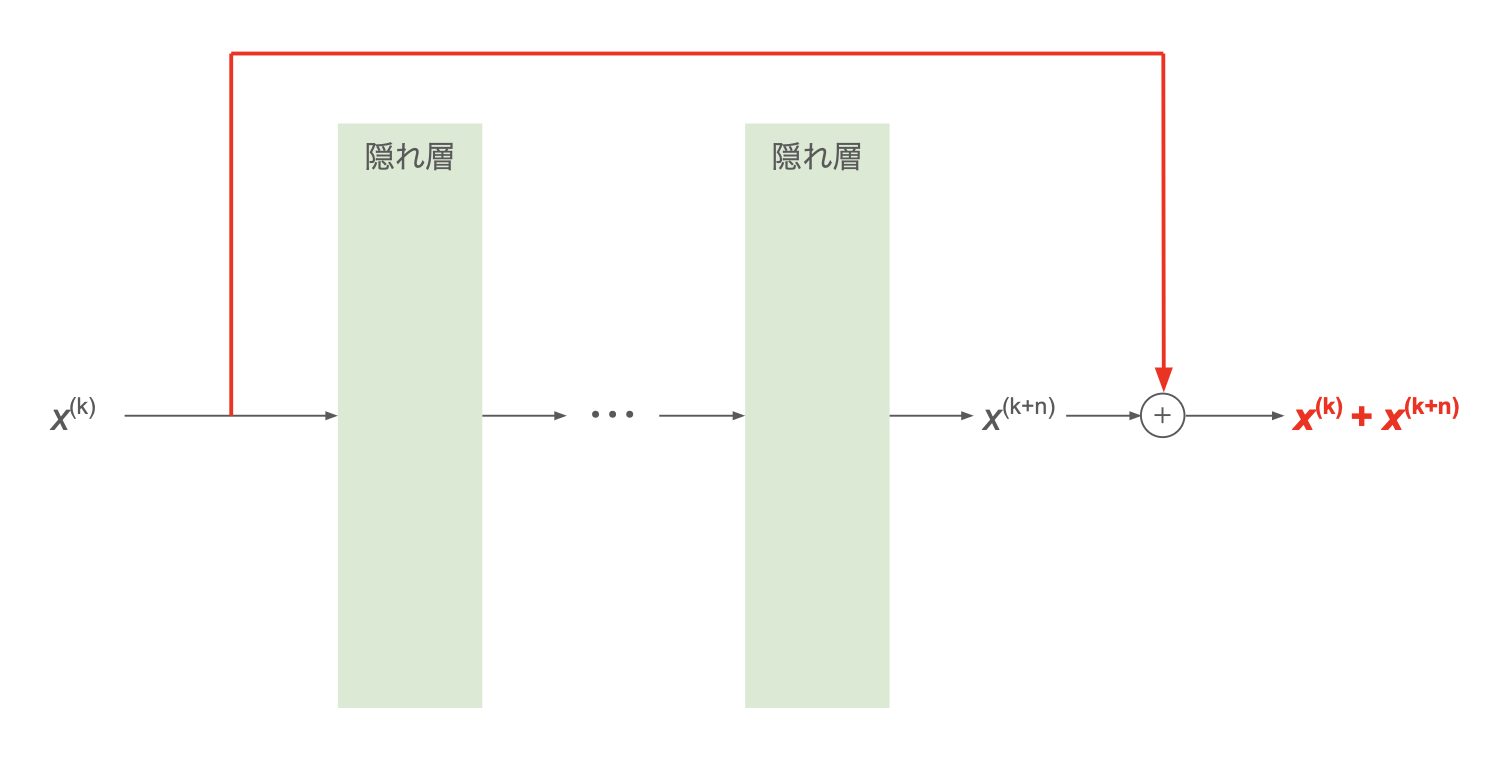
- メリット:
- 迂回路を逆伝播する誤差も隠れ層を回避するため、(回避した層による)勾配消失の影響を受けない
- 回避された隠れ層の部分の学習がうまくいかなくても、元の情報が次へ伝わるため、「壊れにくい」構造になる
- デメリット:
- 多用しすぎると情報が過剰に伝達され、層を深くするメリットが薄れる場合も
実装・動作確認
多層パーセプトロンによる多クラス分類器を作ってみる。
勾配爆発・勾配消失の防止のため、Batch Normalization を適用する。
コード
各層のクラス
全結合層:
活性化関数:
SoftMax 関数:
損失関数(Cross-Entropy Loss):
Batch Normalization:
Dropout:
分類器本体
動作確認
データ生成:
結果の描画:
# データ作成
N_train = 600
N_test = 300
X, Y = ClassificationToyData().circles(N_train + N_test)
X_train, Y_train = X[:N_train], Y[:N_train]
X_test, Y_test = X[N_train:], Y[N_train:]
# モデル初期化・学習
model = MLPClassifier(X_train, Y_train, X_test, Y_test, H=20, L=2, dropout=0, activation_func=ReLU)
model.train(epoch=20, mini_batch=20, eta=0.01, log_interval=1)
# 結果の描画
plt.figure(figsize=(16, 4))
plt.subplots_adjust(wspace=0.2, hspace=0.4)
plt.subplot(1, 3, 1)
draw_decision_boundary(model, X, Y)
plt.subplot(1, 3, 2)
model.plot_accuracy()
plt.subplot(1, 3, 3)
model.plot_loss()
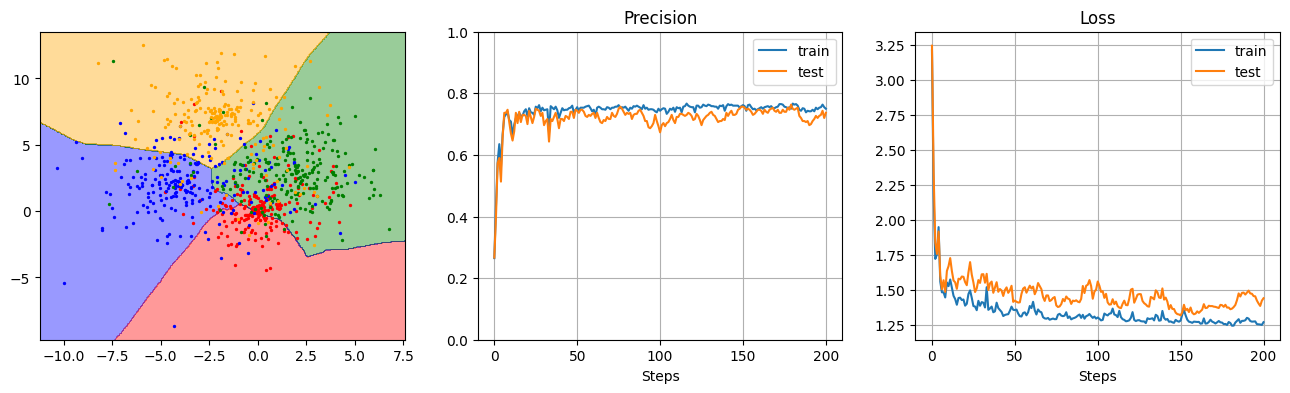
実験・調査
隠れ層の深さの比較
- 隠れ層の数(深さ):0, 1, 2, 3
- 隠れ層のニューロン数:20
- 活性化関数:ReLU
- Dropout:0(なし)
の条件下で隠れ層の深さを変えて結果を見てみる。
Ls = [0, 1, 2, 3]
n = len(Ls)
plt.figure(figsize=(16, 4*n))
plt.subplots_adjust(wspace=0.2, hspace=0.4)
for i in range(n):
L = Ls[i]
model = MLPClassifier(X_train, Y_train, X_test, Y_test, H=20, L=L, dropout=0, activation_func=ReLU)
model.train(epoch=20, mini_batch=20, eta=0.01, log_interval=1)
plt.subplot(n, 3, i*3+1)
draw_decision_boundary(model, X, Y, title='{} hidden layers'.format(L))
plt.subplot(n, 3, i*3+2)
model.plot_precision()
plt.subplot(n, 3, i*3+3)
model.plot_loss()
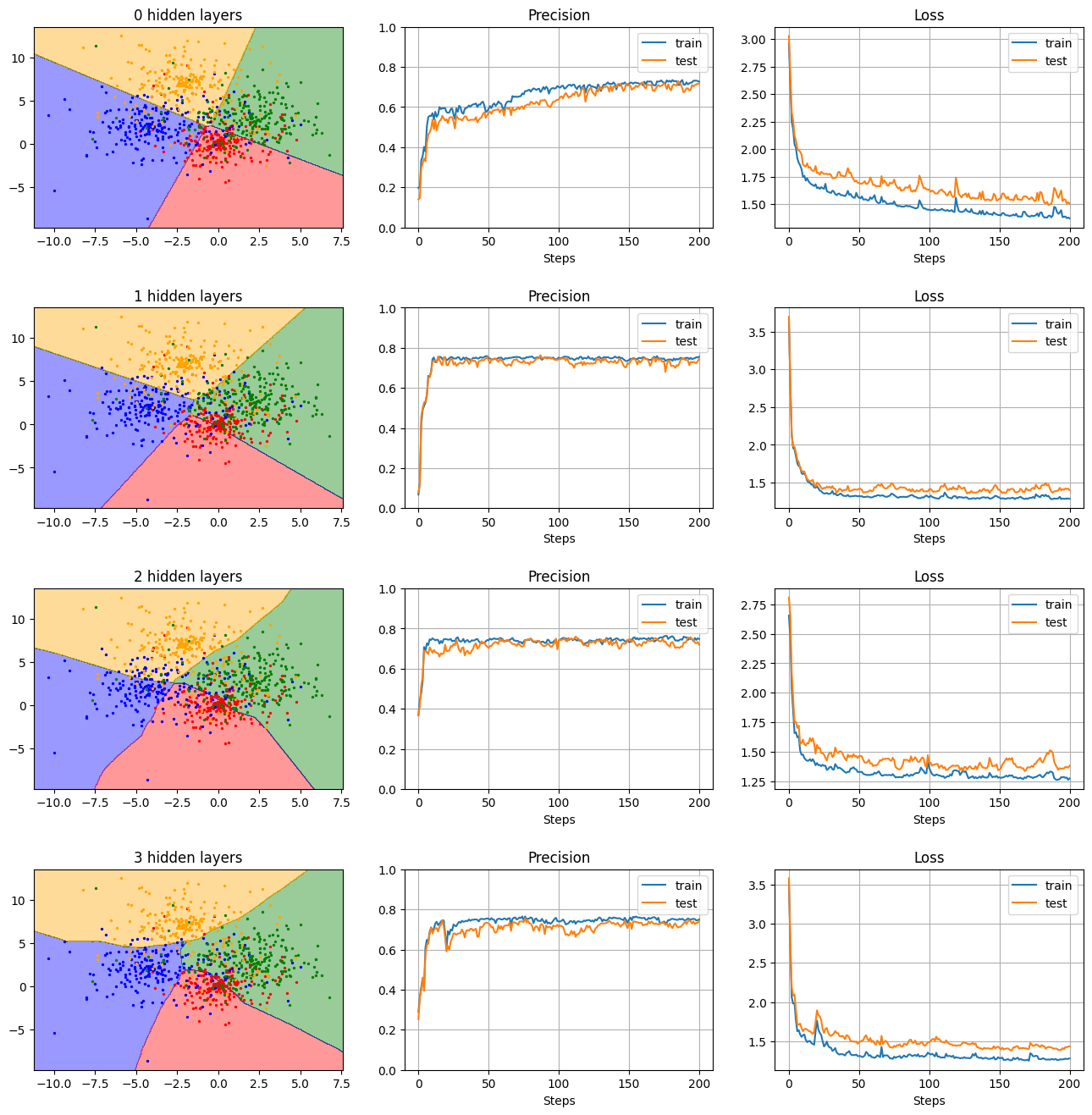
→ 隠れ層が増えるほど、複雑な境界に対応できる様子がわかる。ただ、今回試したようなシンプルなトイデータでは、2〜4層で大きな差は見られない。
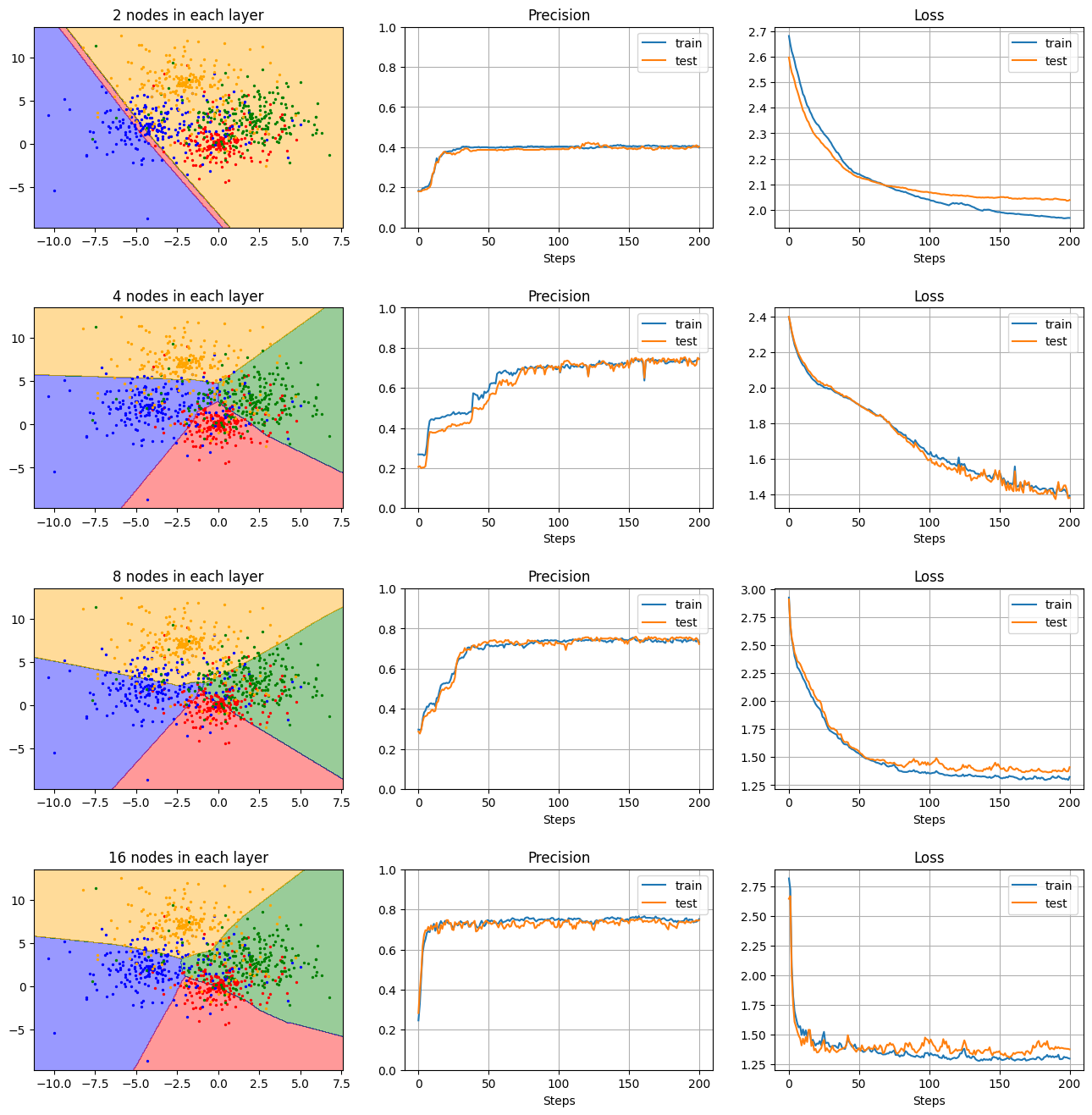
隠れ層のニューロン数の比較
- 隠れ層の数(深さ):2
- 隠れ層のニューロン数:2, 4, 8, 16
- 活性化関数:ReLU
- Dropout:0(なし)
の条件下で、隠れ層が持つニューロン数を変えて結果を見てみる。
Hs = [2, 4, 8, 16]
n = len(Hs)
plt.figure(figsize=(16, 4*n))
plt.subplots_adjust(wspace=0.2, hspace=0.4)
for i in range(n):
H = Hs[i]
model = MLPClassifier(X_train, Y_train, X_test, Y_test, H=H, L=2, dropout=0, activation_func=ReLU)
model.train(epoch=20, mini_batch=20, eta=0.01, log_interval=1)
plt.subplot(n, 3, i*3+1)
draw_decision_boundary(model, X, Y, title='{} nodes in each layer'.format(H))
plt.subplot(n, 3, i*3+2)
model.plot_precision()
plt.subplot(n, 3, i*3+3)
model.plot_loss()
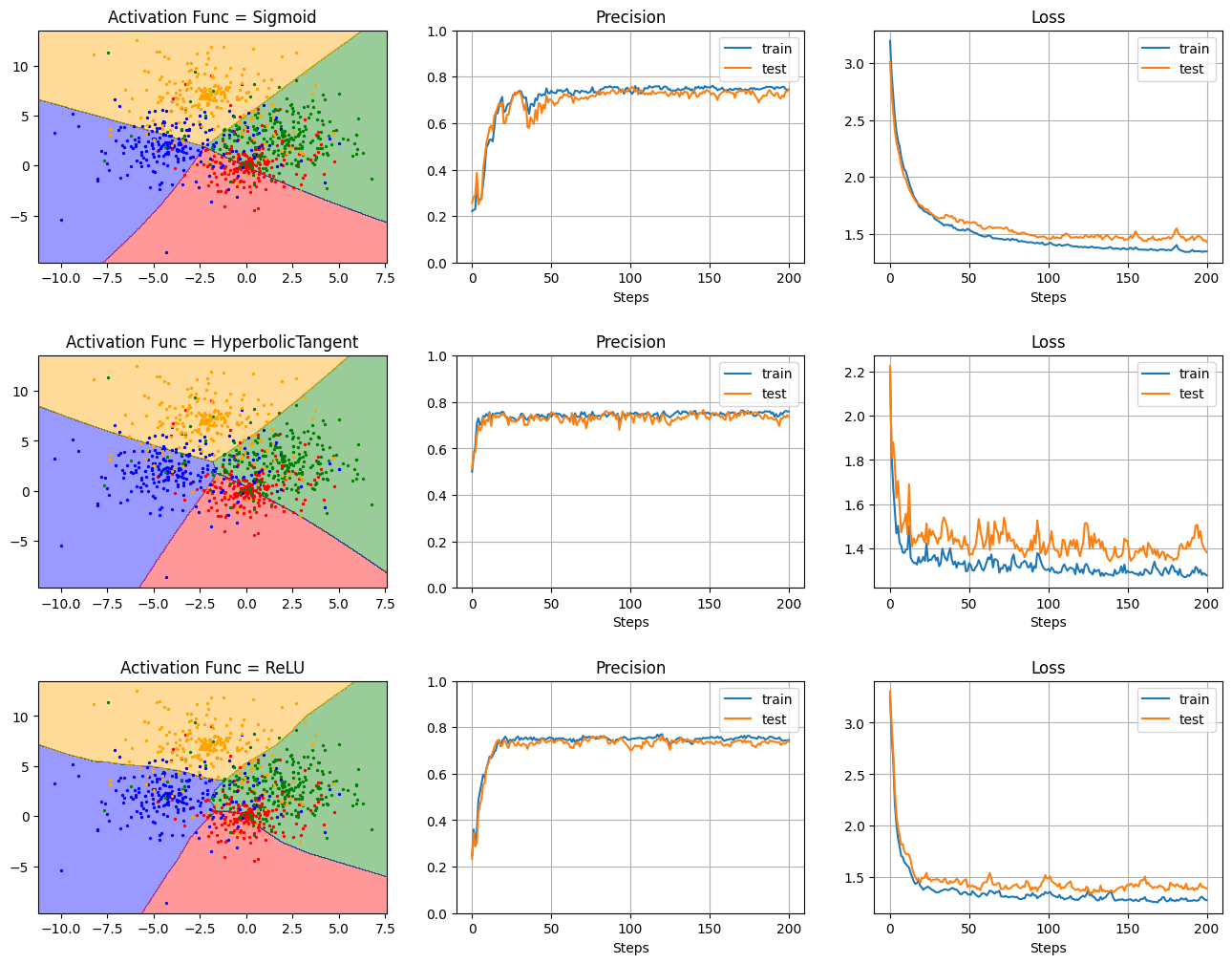
活性化関数の比較
- 隠れ層の数(深さ):2
- 隠れ層のニューロン数:20
- 活性化関数:Sigmoid / Hyperbolic Tangent / ReLU
- Dropout:0(なし)
の条件下で、活性化関数を変えて結果を見てみる。
activation_funcs = [Sigmoid, HyperbolicTangent, ReLU]
n = len(activation_funcs)
plt.figure(figsize=(16, 4*len(activation_funcs)))
plt.subplots_adjust(wspace=0.2, hspace=0.4)
for i in range(n):
F = activation_funcs[i]
model = MLPClassifier(X_train, Y_train, X_test, Y_test, H=20, L=2, dropout=0, activation_func=F)
model.train(epoch=20, mini_batch=20, eta=0.01, log_interval=1)
plt.subplot(n, 3, i*3+1)
draw_decision_boundary(model, X, Y, title='Activation Func = {}'.format(F.__name__))
plt.subplot(n, 3, i*3+2)
model.plot_precision()
plt.subplot(n, 3, i*3+3)
model.plot_loss()
Dropout と過学習抑制
- 隠れ層の数(深さ):2
- 隠れ層のニューロン数:20
- 活性化関数:ReLU
- Dropout:0(なし), 0.1, 0.2, 0.3, 0.4, 0.5
の条件下で、Dropout の利用の有無を変えて結果を見てみる。
dropout = [0, 0.1, 0.2, 0.3, 0.4, 0.5]
n = len(dropout)
plt.figure(figsize=(16, 4*n))
plt.subplots_adjust(wspace=0.2, hspace=0.4)
for i in range(n):
do = dropout[i]
model = MLPClassifier(X_train, Y_train, X_test, Y_test, H=20, L=2, dropout=do, activation_func=ReLU)
model.train(epoch=40, mini_batch=20, eta=0.01, log_interval=1)
plt.subplot(n, 3, i*3+1)
draw_decision_boundary(model, X, Y, title='Dropout = {}'.format(do))
plt.subplot(n, 3, i*3+2)
model.plot_precision()
plt.subplot(n, 3, i*3+3)
model.plot_loss()

→ 1度だけの学習では、dropout の有無で有意な差があるかイマイチ分からない…
次に、いろいろな dropout の値で繰り返し学習して、学習データとテストデータのコスト関数の差を計算してみる:
# 繰り返し学習
T = 100
dropout = [0, 0.1, 0.2, 0.3, 0.4, 0.5]
n = len(dropout)
loss_train = np.zeros((n, T))
loss_test = np.zeros((n, T))
p_train = np.zeros((n, T))
p_test = np.zeros((n, T))
for i in range(n):
do = dropout[i]
for t in tqdm(range(T)):
model = MLPClassifier(X_train, Y_train, X_test, Y_test, H=20, L=2, dropout=do, activation_func=ReLU)
model.train(epoch=100, mini_batch=20, eta=0.01, log_interval=10, progress_bar=False)
loss_train[i,t] = model.loss_train[-1]
loss_test[i,t] = model.loss_test[-1]
p_train[i,t] = model.precision_train[-1]
p_test[i,t] = model.precision_test[-1]
loss_diff = loss_test - loss_train
p_diff = p_train - p_test
# 結果の描画
plt.figure(figsize=(10, 8))
plt.subplots_adjust(wspace=0.4, hspace=0.2)
plt.subplot(2, 2, 1)
plt.errorbar(dropout, p_train.mean(axis=1), p_train.std(axis=1), capsize=3, fmt='.', markersize=10, ecolor="black", elinewidth=0.5, markeredgecolor="black", color="w")
plt.plot(dropout, p_train.mean(axis=1), label='train')
plt.errorbar(dropout, p_test.mean(axis=1), p_test.std(axis=1), capsize=3, fmt='.', markersize=10, ecolor="black", elinewidth=0.5, markeredgecolor="black", color="w")
plt.plot(dropout, p_test.mean(axis=1), label='test')
plt.xlabel('Dropout', size=13)
plt.ylabel(r'$Precision$', size=13)
plt.legend()
plt.grid()
plt.subplot(2, 2, 2)
plt.errorbar(dropout, p_diff.mean(axis=1), p_diff.std(axis=1), capsize=3, fmt='.', markersize=10, ecolor="black", elinewidth=0.5, markeredgecolor="black", color="w")
plt.plot(dropout, p_diff.mean(axis=1))
plt.xlabel('Dropout', size=13)
plt.ylabel(r'$Precision_{train} - Precision_{test}$', size=13)
plt.grid()
plt.subplot(2, 2, 3)
plt.errorbar(dropout, loss_train.mean(axis=1), loss_train.std(axis=1), capsize=3, fmt='.', markersize=10, ecolor="black", elinewidth=0.5, markeredgecolor="black", color="w")
plt.plot(dropout, loss_train.mean(axis=1), label='train')
plt.errorbar(dropout, loss_test.mean(axis=1), loss_test.std(axis=1), capsize=3, fmt='.', markersize=10, ecolor="black", elinewidth=0.5, markeredgecolor="black", color="w")
plt.plot(dropout, loss_test.mean(axis=1), label='test')
plt.xlabel('Dropout', size=13)
plt.ylabel(r'$Loss$', size=13)
plt.legend()
plt.grid()
plt.subplot(2, 2, 4)
plt.errorbar(dropout, loss_diff.mean(axis=1), loss_diff.std(axis=1), capsize=3, fmt='.', markersize=10, ecolor="black", elinewidth=0.5, markeredgecolor="black", color="w")
plt.plot(dropout, loss_diff.mean(axis=1))
plt.xlabel('Dropout', size=13)
plt.ylabel(r'$(Loss_{test} - Loss_{train}) / Loss_{train}$', size=13)
plt.grid()
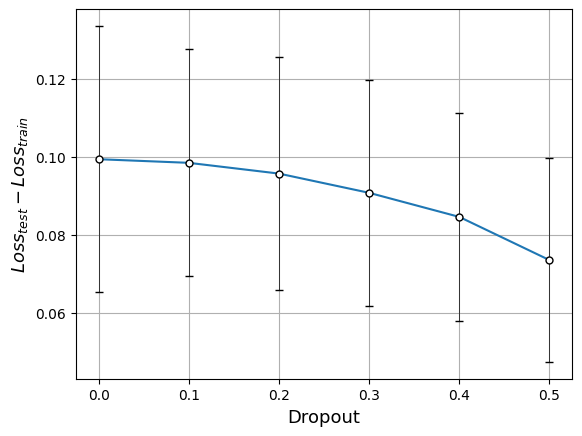
【注】
- エラーバーの長さはそれぞれ、$\sigma$ を標準偏差として $\pm 1\sigma$ の範囲
- Dropout による情報落ちで損失関数自体が大きくなるため、損失関数の差分 $Loss_\mathrm{test}-Loss_\mathrm{train}$ を $Loss_\mathrm{train}$ で割ってスケールを揃え、過学習抑制の効果が見えやすいようにしている
- Dropout を大きくするにつれて、train と test の損失関数の差分は有意に減少(右下図)
- 分類精度の差分も小さくなっているように見える(右上図)が、分散も大きいので有意差とは言いにくいかも
- しかし情報が欠落する分、損失関数自体の値は大きくなり(左下図)、分類精度も低下(左上図)
 Technical Note - 多層パーセプトロン
Technical Note - 多層パーセプトロン